Carleman Linearization 

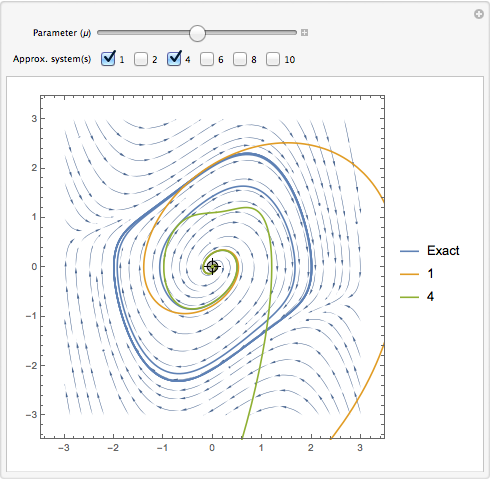
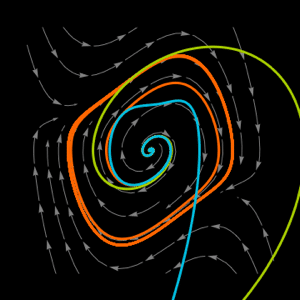
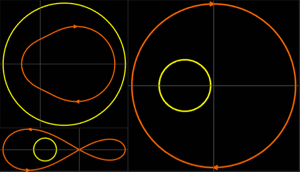
The rich dynamics of nonlinear systems can only be partially captured by approximate linearizations. Evaluate the effectiveness of different orders of Carleman linearization at various points in the phase space of a Van der Pol oscillator.

The model of a Van der Pol oscillator.

In[1]:=

X vanderpol[\[Mu]_] := AffineStateSpaceModel[ {{Subscript[x, 2], -Subscript[x, 1] - \[Mu] (-1 + \!\(\*SubsuperscriptBox[\(x\), \(1\), \(2\)]\)) Subscript[x, 2]}, {{ }, {}}}, {Subscript[x, 1], Subscript[x, 2]}, {}, {Automatic, Automatic}, Automatic , SamplingPeriod -> None]

Its response for 100 time units from an initial point p.

In[2]:=

X vanderpolResponse[\[Mu]_, p_] := OutputResponse[{vanderpol[\[Mu]], p}, {}, {t, 0, 100}]

Its phase portrait.

In[3]:=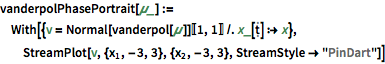

X vanderpolPhasePortrait[\[Mu]_] := With[{v = Normal[vanderpol[\[Mu]]][[1, 1]] /. x_[\[FormalT]] :> x}, StreamPlot[v, {Subscript[x, 1], -3, 3}, {Subscript[x, 2], -3, 3}, StreamStyle -> "PinDart"]]

The response of a Carleman-linearized system with approximation order n.

In[4]:=

X approxResponse[\[Mu]_, p_, n_] := With[{\[ScriptCapitalC] = CarlemanLinearize[vanderpol[\[Mu]], n]}, OutputResponse[{\[ScriptCapitalC]["TransformedSystem"], Last /@ \[ScriptCapitalC]["EmbeddingTransformation"] /. Thread[{Subscript[x, 1], Subscript[x, 2]} -> p]}, {}, {t, 0, 100}]]

Visualize the actual and approximated trajectories from various initial points.

In[5]:=

X Manipulate[ Show[vanderpolPhasePortrait[\[Mu]], ParametricPlot[ Evaluate[{vanderpolResponse[\[Mu], p]}~ Join~(approxResponse[\[Mu], p, #] & /@ n)], {t, 0, 100}, PlotLegends -> Join[{"Exact"}, n]], ImageSize -> Medium], {{p, {0.01, 0}}, {-3, -3}, {3, 3}, Locator}, {{\[Mu], 0.6, "Parameter (\[Mu])"}, 0, 1.2, 0.1}, {{n, {1, 4}, "Approx. system(s)"}, CheckboxBar[Dynamic@n, {1, 2, 4, 6, 8, 10}] &}, SaveDefinitions -> True, AutorunSequencing -> {1, 2}]

Play Animation Stop Animation