Example of a General Nonlinear System
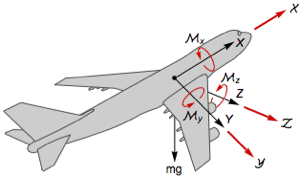
Physical systems where the control inputs appear nonlinearly are rather uncommon. They are, however, indispensable in the high-fidelity modeling of aircraft dynamics, where the control surfaces such as the elevator, aileron, and rudder affect the aerodynamic forces and moments of the aircraft in a nonlinear manner.
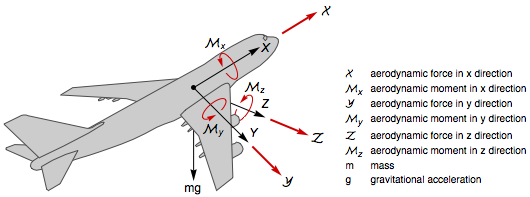 |
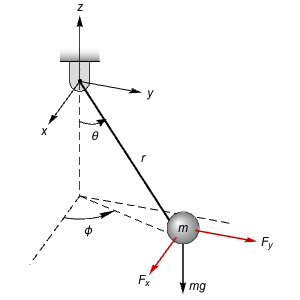
The six-degree-of-freedom model in body coordinates, where are the inertia terms.
| In[1]:= | 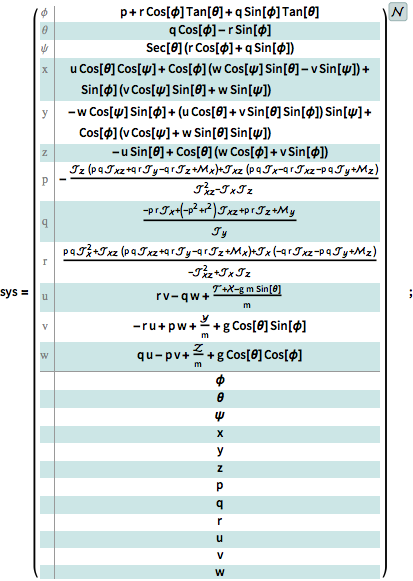 X |
The longitudinal dynamics are the dynamics for states 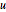 ,
, 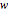 ,
, 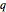 , and
, and 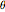 :
:
| In[2]:= | X |
| Out[2]= |  |
The lateral dynamics are the dynamics for the states 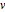 ,
, 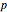 ,
, 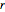 , and
, and 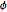 :
:
| In[3]:= | X |
| Out[3]= |  |