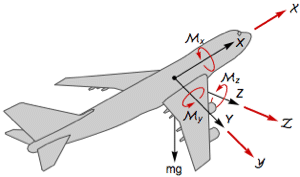
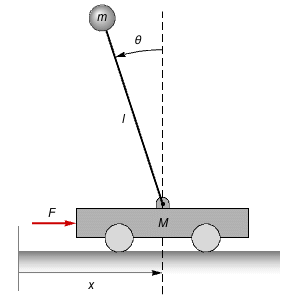
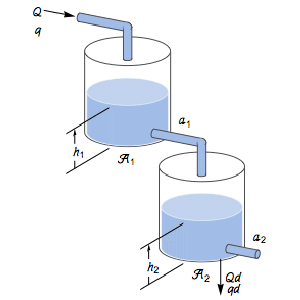
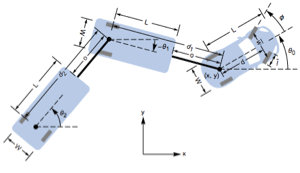
Controllability Decomposition 

The controllability decomposition reveals the inner structure and the reachable subspace of the system. The subspace can be visualized for second- and third-order systems and in general is a manifold.

An affine system. »

In[1]:=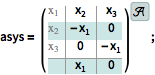

X asys = AffineStateSpaceModel[ {{Subscript[x, 2], -Subscript[x, 1], 0}, {{ Subscript[x, 3] }, {0 }, {-Subscript[x, 1] }}, {Subscript[x, 1]}, {{ 0 }}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}, Automatic, {Automatic}, Automatic , SamplingPeriod -> None];

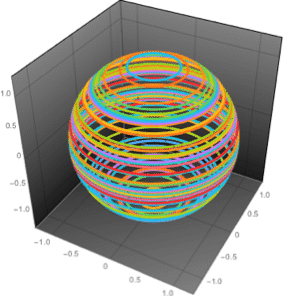
Its reachable subspace is a sphere.

In[2]:=

X {{p1, p2}, csys} = ControllableDecomposition[ asys, {Subscript[z, 1], Subscript[z, 2], Subscript[z, 3]}];

In[3]:=

X p2[[-1]]

Out[3]=

The transformation reveals that it is confined to a specific sphere because .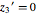

In[4]:=

X StateSpaceTransform[asys, {p1, Flatten@p2}]

Out[4]=

The system starts and remains on the same sphere for all inputs.

In[5]:=

X Manipulate[ x0 = Table[ With[{xyz = RandomVariate[NormalDistribution[], 3]}, r xyz/Norm[xyz]], {n}]; sr = Table[StateResponse[{asys, x}, u, {t, 0, 10}], {x, x0}]; ParametricPlot3D[sr, {t, 0, 10}, PlotRange -> 1.3, ImageSize -> Medium], {{u, 0, "System input"}, {0, UnitStep[t], Sin[t], t}}, {{r, 1.2, "Radius of the sphere"}, 1, 1.3, 0.1}, {{n, 50, "No of sample points"}, 1, 100}, SaveDefinitions -> True]

Play Animation Stop Animation