Asymptotic Output Tracking with Estimator
Design a controller for a cardiac pacemaker to maintain a healthy ECG signal. The controller has to incorporate an estimator since not all signals are measured. »
A third-order heartbeat model.
| In[1]:= |  X |
With completely zero stimuli, the ECG signal is zero.
| In[2]:= |  X |
| Out[2]= |  |
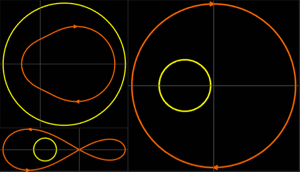
The model reveals some zero dynamics involving states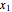 
and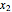 
.
| In[3]:= |  X |
| In[4]:= |  X |
| Out[4]= |  |
The zero dynamics are well behaved.
| In[5]:= |  X |
| Out[5]= |  |
A reference data for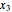 
is obtained from physionet.org.
| In[6]:= |  X |
Compute the tracking controller.
| In[7]:= |  X |
| Out[7]= |  |
Compute a set of estimator gains.
| In[8]:= |  X |
| Out[8]= |  |
The complete controller.
| In[9]:= |  X |
| Out[9]= |  |
The simulation shows that the tracking has been achieved.
| In[10]:= |  X |
| In[11]:= |  X |
| Out[11]= |  |
