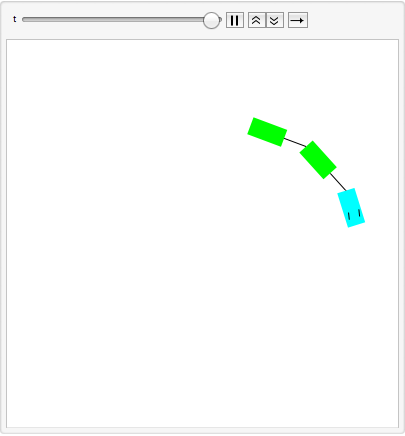
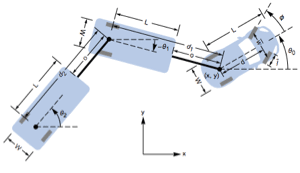
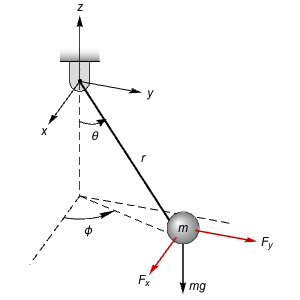
Controllability 

A car with two trailers is controllable. The approximately linearized model fails to reveal the controllability, while the affine model does. »

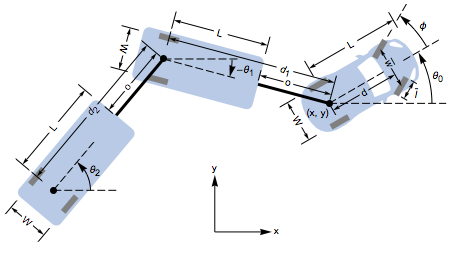The affine model.

In[1]:=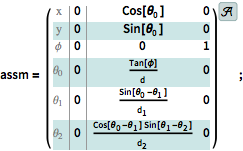

X assm = AffineStateSpaceModel[ {{0, 0, 0, 0, 0, 0}, {{ Cos[Subscript[\[Theta], 0]], 0 }, {Sin[Subscript[\[Theta], 0]], 0 }, {0, 1 }, {Tan[\[Phi]]/d, 0 }, {Sin[Subscript[\[Theta], 0] - Subscript[\[Theta], 1]]/ Subscript[d, 1], 0 }, {( Cos[Subscript[\[Theta], 0] - Subscript[\[Theta], 1]] Sin[ Subscript[\[Theta], 1] - Subscript[\[Theta], 2]])/Subscript[d, 2], 0 }}}, {x, y, \[Phi], Subscript[\[Theta], 0], Subscript[\[Theta], 1], Subscript[\[Theta], 2]}, Automatic, {Automatic, Automatic, Automatic, Automatic, Automatic, Automatic}, Automatic , SamplingPeriod -> None];

The linear model is not controllable.

In[2]:=

X ssm = StateSpaceModel[assm]

Out[2]=

In[3]:=

X ControllableModelQ[ssm]

Out[3]=

The affine model shows that the system is controllable.

In[4]:=

X ControllableModelQ[assm]

Out[4]=

Simulate the affine system for a set of input signals.

In[5]:=

X L = 1; W = 0.5; o = 0.65; d = 0.8; \!\(\*OverscriptBox[\(l\), \(_\)]\) = 0.2; \!\(\*OverscriptBox[\(w\), \(_\)]\) = 0.3;

In[6]:=

X {Subscript[x, r], Subscript[y, r], Subscript[\[Phi], r], Subscript[\[Theta], r0], Subscript[\[Theta], r1], Subscript[\[Theta], r2]} = StateResponse[{assm /. {Subscript[d, 1] -> o + L, Subscript[d, 2] -> o + L}, {0, 0, 0, 0, 0, 0}}, {0.1, -Piecewise[{{0.1, 0 <= t <= 1}, {0.1, 3 <= t <= 4}}, 0]}, {t, 0, 350}];

Visualize its motion.

show complete Wolfram Language inputhide input

In[7]:=

X polygon[{x_, y_}, th_] := Polygon[{{x + W/2 Sin[th], y - W/2 Cos[th]}, {x - W/2 Sin[th], y + W/2 Cos[th]}, {x - W/2 Sin[th] + L Cos[th], y + W/2 Cos[th] + L Sin[th]}, {x + W/2 Sin[th] + L Cos[th], y - W/2 Cos[th] + L Sin[th]}}] line[{x_, y_}, l_, th_] := Line[{{x, y}, {x - l Cos[th], y - l Sin[th]}}] Animate[ Graphics[{Cyan, polygon[{Subscript[x, r], Subscript[y, r]}, Subscript[\[Theta], r0]], Black, line[{Subscript[x, r] + d Cos[Subscript[\[Theta], r0]] - \!\(\*OverscriptBox[\(w\), \(_\)]\)/2 Sin[Subscript[\[Theta], r0]], Subscript[y, r] + d Sin[Subscript[\[Theta], r0]] + \!\(\*OverscriptBox[\(w\), \(_\)]\)/2 Cos[Subscript[\[Theta], r0]]}, \!\(\*OverscriptBox[\(l\), \(_\)]\), Subscript[\[Phi], r] + Subscript[\[Theta], r0]], line[{Subscript[x, r] + d Cos[Subscript[\[Theta], r0]] + \!\(\*OverscriptBox[\(w\), \(_\)]\)/2 Sin[Subscript[\[Theta], r0]], Subscript[y, r] + d Sin[Subscript[\[Theta], r0]] - \!\(\*OverscriptBox[\(w\), \(_\)]\)/2 Cos[Subscript[\[Theta], r0]]}, \!\(\*OverscriptBox[\(l\), \(_\)]\), Subscript[\[Phi], r] + Subscript[\[Theta], r0]], line[{Subscript[x, r], Subscript[y, r]}, o, Subscript[\[Theta], r1]], Green, polygon[{Subscript[x, r] - (L + o) Cos[Subscript[\[Theta], r1]], Subscript[y, r] - (L + o) Sin[Subscript[\[Theta], r1]]}, Subscript[\[Theta], r1]], Black, line[{Subscript[x, r] - (L + o) Cos[Subscript[\[Theta], r1]], Subscript[y, r] - (L + o) Sin[Subscript[\[Theta], r1]]}, L, Subscript[\[Theta], r2]], Green, polygon[{Subscript[x, r] - (L + o) Cos[Subscript[\[Theta], r1]] - (L + o) Cos[ Subscript[\[Theta], r2]], Subscript[y, r] - (L + o) Sin[Subscript[\[Theta], r1]] - (L + o) Sin[ Subscript[\[Theta], r2]]}, Subscript[\[Theta], r2]] }, PlotRange -> {{-5, 5}, {-9, 1}}, ImageSize -> Medium] // Evaluate, {t, 0, 300}, AnimationRate -> 25, AnimationRepetitions -> 1, SaveDefinitions -> True]

Play Animation Stop Animation