Carleman線形化 

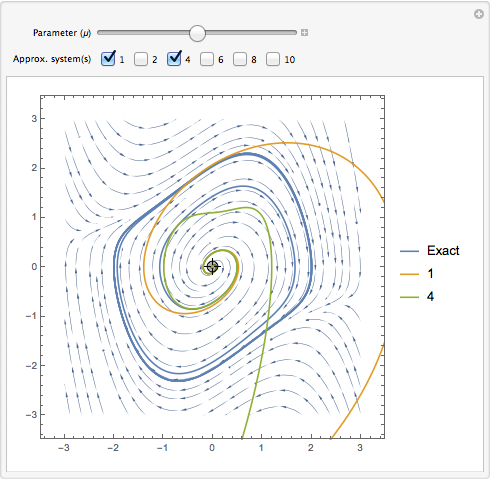
非線形系の豊かな動力学は近似線形化ではほんの部分的にしか把握できない．ファン・デル・ポル(van der Pol)振動子の位相空間におけるいくつかの点で異なる次数のCarleman線形化の効率を評価する．

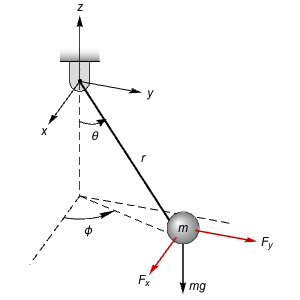
ファン・デル・ポル振動子のモデル．

In[1]:=

X vanderpol[\[Mu]_] := AffineStateSpaceModel[ {{Subscript[x, 2], -Subscript[x, 1] - \[Mu] (-1 + \!\(\*SubsuperscriptBox[\(x\), \(1\), \(2\)]\)) Subscript[x, 2]}, {{ }, {}}}, {Subscript[x, 1], Subscript[x, 2]}, {}, {Automatic, Automatic}, Automatic , SamplingPeriod -> None]

初期点 p からの100時間単位に対する応答．

In[2]:=

X vanderpolResponse[\[Mu]_, p_] := OutputResponse[{vanderpol[\[Mu]], p}, {}, {t, 0, 100}]

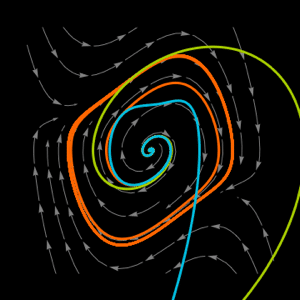
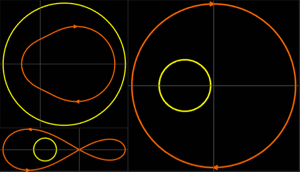
その位相ポートレート．

In[3]:=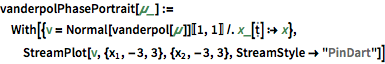

X vanderpolPhasePortrait[\[Mu]_] := With[{v = Normal[vanderpol[\[Mu]]][[1, 1]] /. x_[\[FormalT]] :> x}, StreamPlot[v, {Subscript[x, 1], -3, 3}, {Subscript[x, 2], -3, 3}, StreamStyle -> "PinDart"]]

近似次数 n のCarleman線形化された系の応答．

In[4]:=

X approxResponse[\[Mu]_, p_, n_] := With[{\[ScriptCapitalC] = CarlemanLinearize[vanderpol[\[Mu]], n]}, OutputResponse[{\[ScriptCapitalC]["TransformedSystem"], Last /@ \[ScriptCapitalC]["EmbeddingTransformation"] /. Thread[{Subscript[x, 1], Subscript[x, 2]} -> p]}, {}, {t, 0, 100}]]

さまざまな初期点からの実際の軌道と近似された軌道を可視化する．

In[5]:=

X Manipulate[ Show[vanderpolPhasePortrait[\[Mu]], ParametricPlot[ Evaluate[{vanderpolResponse[\[Mu], p]}~ Join~(approxResponse[\[Mu], p, #] & /@ n)], {t, 0, 100}, PlotLegends -> Join[{"Exact"}, n]], ImageSize -> Medium], {{p, {0.01, 0}}, {-3, -3}, {3, 3}, Locator}, {{\[Mu], 0.6, "Parameter (\[Mu])"}, 0, 1.2, 0.1}, {{n, {1, 4}, "Approx. system(s)"}, CheckboxBar[Dynamic@n, {1, 2, 4, 6, 8, 10}] &}, SaveDefinitions -> True, AutorunSequencing -> {1, 2}]

動画を開始 動画を中止