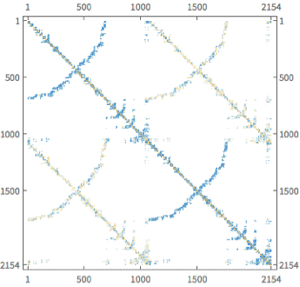
Solve a Complex-Valued Oscillator
Solve a harmonic oscillator 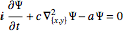 over a 2D disk region. The mass matrix option is given in order to solve the PDE with complex-valued coefficients.
over a 2D disk region. The mass matrix option is given in order to solve the PDE with complex-valued coefficients.
| In[1]:= | 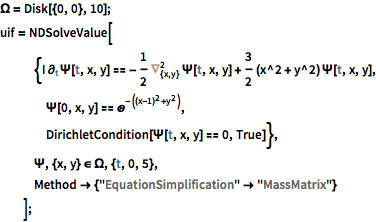 X |
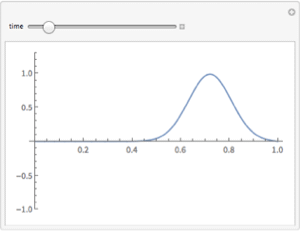
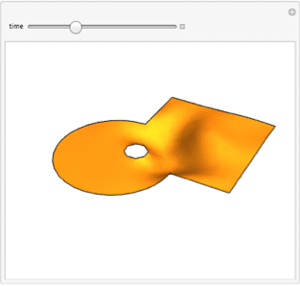
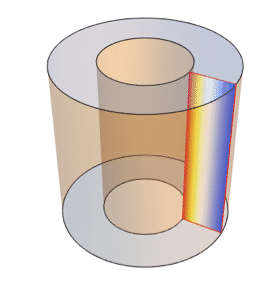
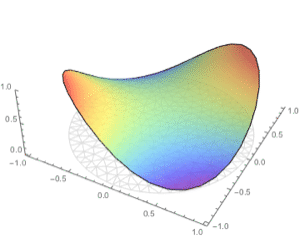
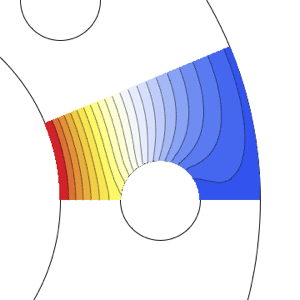
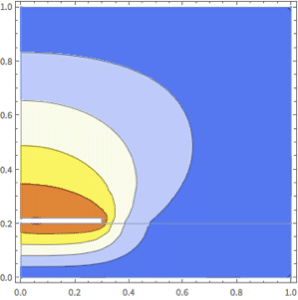
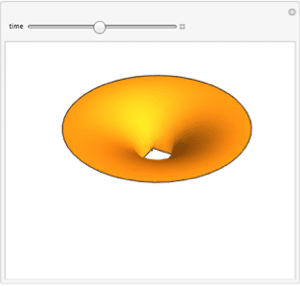
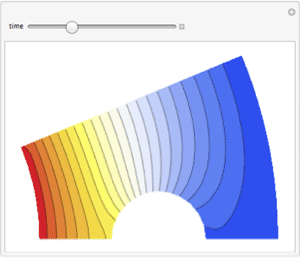
Visualize real and imaginary parts of the result.
| In[2]:= | 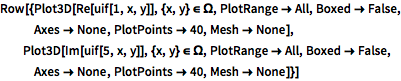 X |
| Out[2]= | 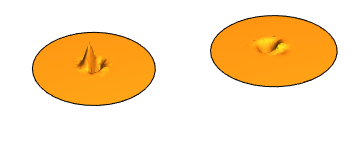 |