分析具有不对称势的斯特姆–刘维算子

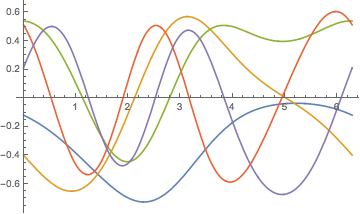
找出斯特姆–刘维算子最小的五个周期特征值和特征函数.

设定斯特姆–刘维算子.

In[1]:=

V[x_] := Cos[x] + x; \[ScriptCapitalL] = -u''[x] - (V''[x] - V'[x]^2) u[x];

设定一个周期性边界条件.

In[2]:=

\[ScriptCapitalB] = u[0] == u[2 \[Pi]];

找出最小的五个周期特征值和特征函数.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 2 \[Pi]}, 5];

查看特征值.

In[4]:=

vals

Out[4]=

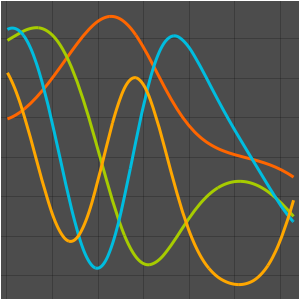
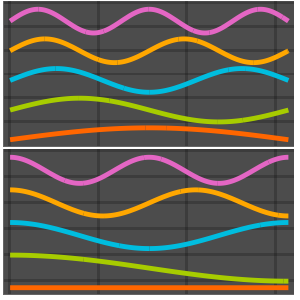
可视化特征函数.

In[5]:=

Plot[funs, {x, 0, 2 \[Pi]}]

Out[5]=