Analise um operador Sturm–Liouville com potencial assimétrico

Encontre os cinco menores valores próprios periódicos e funções próprias de um operador Sturm-Liouville.

Especifique um operador Sturm–Liouville.

In[1]:=

V[x_] := Cos[x] + x; \[ScriptCapitalL] = -u''[x] - (V''[x] - V'[x]^2) u[x];

Especifique uma condição de contorno periódico.

In[2]:=

\[ScriptCapitalB] = u[0] == u[2 \[Pi]];

Encontre os cinco menores valores e funções próprios.

In[3]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 2 \[Pi]}, 5];

Inspecione os valores próprios.

In[4]:=

vals

Out[4]=

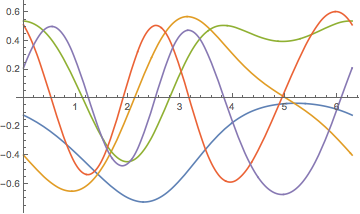
Visualize as funções próprias.

In[5]:=

Plot[funs, {x, 0, 2 \[Pi]}]

Out[5]=