固有関数展開を生成する

区間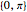でディリクレ境界条件を持つラプラス演算子によって提供される基底について，関数 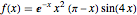を固有関数展開する．

In[1]:=

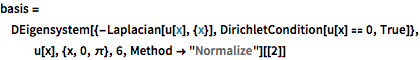
basis = DEigensystem[{-Laplacian[u[x], {x}], DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6, Method -> "Normalize"][[2]]

Out[1]=

関数 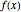に対するフーリエ係数を計算する．

In[2]:=

f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]

In[3]:=

coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] // FullSimplify);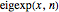

を展開の 次部分和として定義する．

In[4]:=

eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]

In[5]:=

eigexp[x, 3] // N

Out[5]=

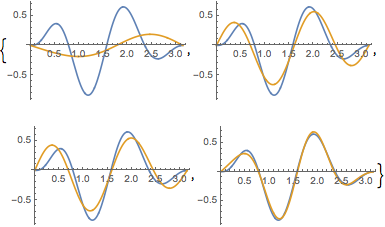
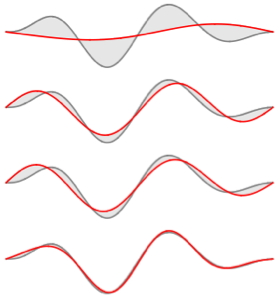
この関数と固有関数展開を，さまざまな の値について比較する．

In[6]:=

Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]

Out[6]=