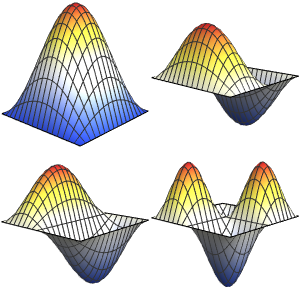
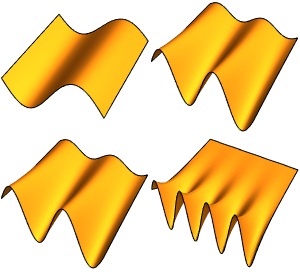
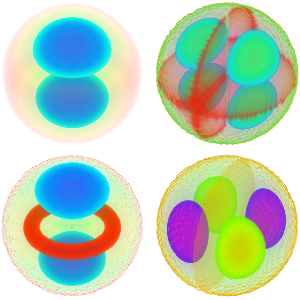
生成特征函数展开式: Wolfram语言 11 的新功能

生成特征函数展开式

在区间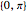上，用一个一维拉普拉斯算子在狄利克雷边界条件下产生的基，计算函数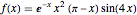的特征函数展开式.

In[1]:=

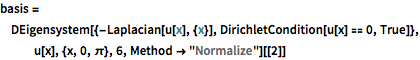
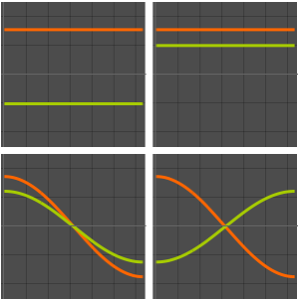
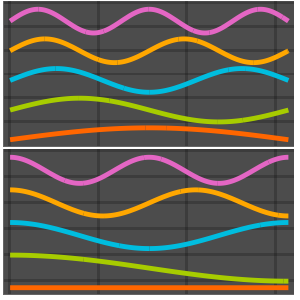
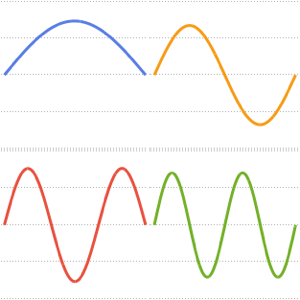
basis = DEigensystem[{-Laplacian[u[x], {x}], 
    DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6, 
   Method -> "Normalize"][[2]]

Out[1]=

计算函数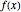的傅里叶系数.

In[2]:=

f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]

In[3]:=

coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] // 
    FullSimplify);

定义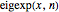为展开式的第个部分和.

In[4]:=

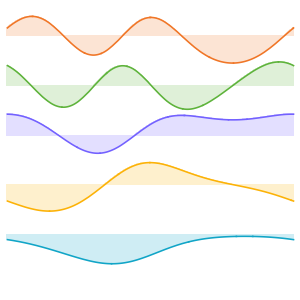
eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]

In[5]:=

eigexp[x, 3] // N

Out[5]=

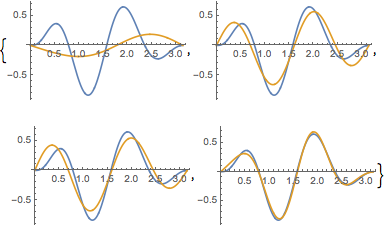
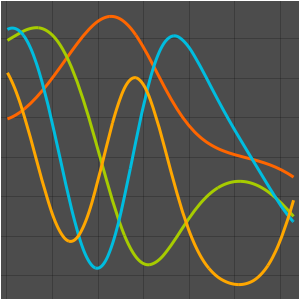
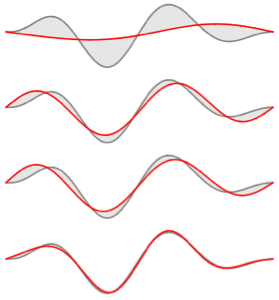
n 取不同值的情况下，将原函数与其特征函数展开式相比较.

In[6]:=

Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]

Out[6]=