Разложение по собственным функциям

Совершим разложение по собственным функциям для функции 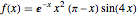на основании оператора Лапласа с граничными условиями Дирихле на отрезке .

In[1]:=

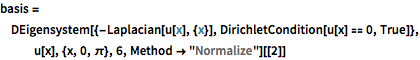
basis = DEigensystem[{-Laplacian[u[x], {x}], DirichletCondition[u[x] == 0, True]}, u[x], {x, 0, \[Pi]}, 6, Method -> "Normalize"][[2]]

Out[1]=

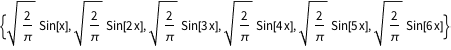
Вычислим коэффициенты Фурье для функции .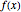

In[2]:=

f[x_] := E^(-x) x^2 (\[Pi] - x) Sin[4 x]

In[3]:=

coeffs = (Table[Integrate[f[x] basis[[i]], {x, 0, Pi}], {i, 6}] // FullSimplify);

Определим 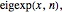как частичнyю суммy разложения.

In[4]:=

eigexp[x_, n_] := Sum[coeffs[[i]] basis[[i]], {i, n}]

In[5]:=

eigexp[x, 3] // N

Out[5]=

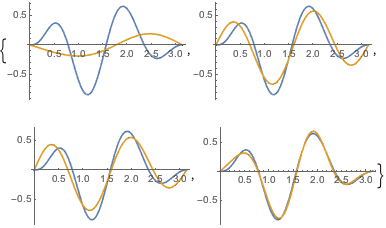
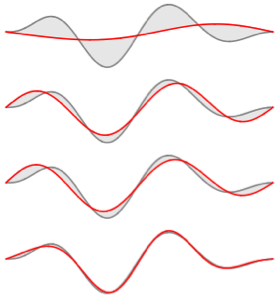
Сравним функцию с ее разложением по собственным функциям для различных значений .

In[6]:=

Table[Plot[{f[x], eigexp[x, i]} // Evaluate, {x, 0, Pi}], {i, 3, 6}]

Out[6]=