Investigate a Laplace Equation on a Torus: New in Wolfram Language 11

Investigate a Laplace Equation on a Torus

Find the five smallest eigenvalues and eigenfunctions of a Laplace equation on a square torus with a Dirichlet constraint.

Specify periodic boundary conditions on a square of length 1.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

Specify a value at the origin. By the periodic conditions, this must also be the value at the other three corners of the square.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

Compute the eigenvalues and eigenfunctions.

In[3]:=

{vals, funs} = 
  NDEigensystem[
   Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], 
   u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

Inspect the eigenvalues.

In[4]:=

vals

Out[4]=

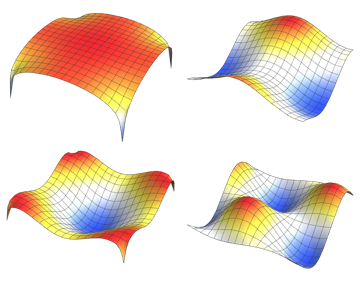
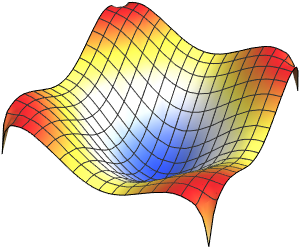
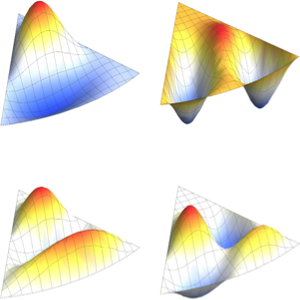
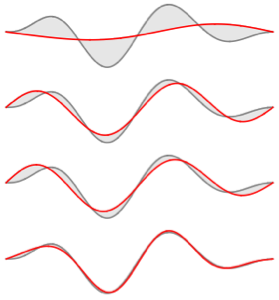
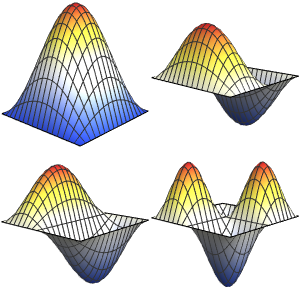
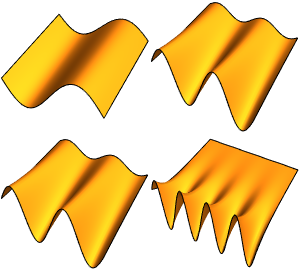
Visualize the eigenfunctions.

show complete Wolfram Language input

In[5]:=

ImageCollage[
 Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 
    ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, 
    PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ 
  funs, Background -> Transparent]

Out[5]=