制約条件付きのラプラス演算子の固有値問題を解く

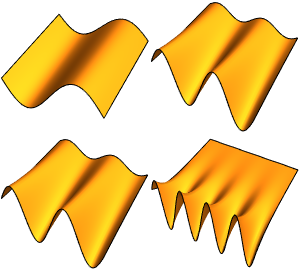
一次元領域上で，同次ディリクレ(Dirichlet)境界条件で制約されたラプラス方程式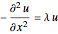 の固有値と固有関数を小さい方から4個求める．

ラプラス演算子を指定する．

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

ディリクレ境界条件を設定する．

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

固有値を数値的に求める．

In[3]:=

NDEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, \[Pi]}, 4]

Out[3]=

固有値と固有関数を数値的に求める．

In[4]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, \[Pi]}, 4];

固有値を調べる．

In[5]:=

vals

Out[5]=

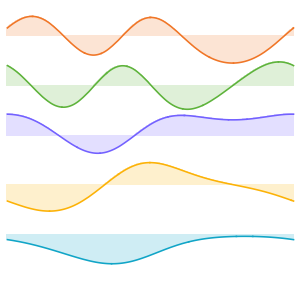
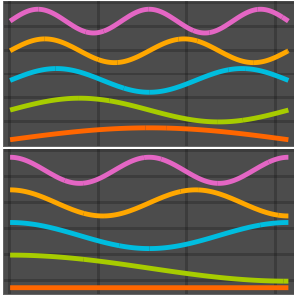
固有関数を可視化する．

In[6]:=

Plot[Evaluate[funs], {x, 0, \[Pi]}]

Out[6]=