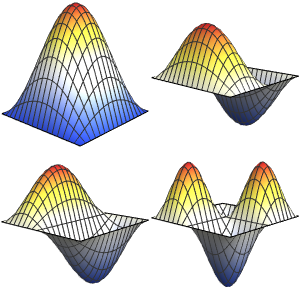
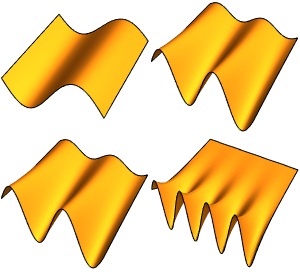
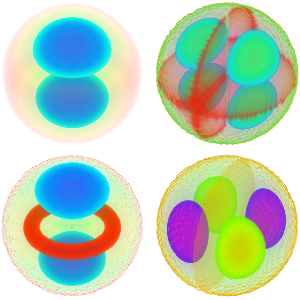
求解有约束的拉普拉斯算子的特征值问题

在齐次狄利克雷边界条件约束下求一维区域上拉普拉斯方程 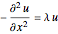最小的四个特征值和特征函数.

设定拉普拉斯算子.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

设定狄利克雷边界条件.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

数值法求解特征值.

In[3]:=

NDEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, \[Pi]}, 4]

Out[3]=

数值法求解特征值和特征函数.

In[4]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, \[Pi]}, 4];

查看特征值.

In[5]:=

vals

Out[5]=

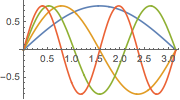
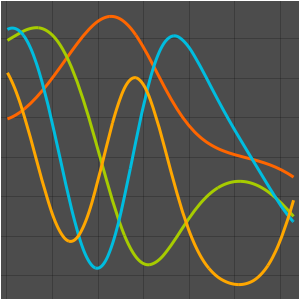
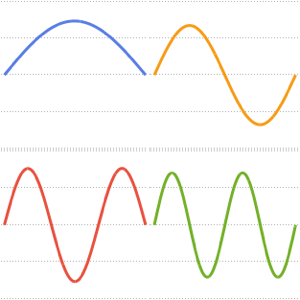
可视化特征函数.

In[6]:=

Plot[Evaluate[funs], {x, 0, \[Pi]}]

Out[6]=