Wolfram Language™

Herzleiden-Datenanalyse

Datenanalyse ist ein Prozess des Extrahierens, Präsentierens und Modellierens auf Basis von Informationen aus erhobenen numerischen Daten. In diesem Beispiel demonstrieren wir einen Arbeitsablauf der Datenanalyse in der Wolfram Language. Der verwendete Datensatz stammt vom UCI Machine Learning Repository, das die Diagnosedaten von 1541 Patienten mit Herzleiden sammelt.

Importieren Sie Diagnosedaten zu Herzkrankheiten und parsen Sie diese, so dass jede Zeile einem anderen Patienten und jede Säule einem anderen Attribut entspricht.

In[1]:=

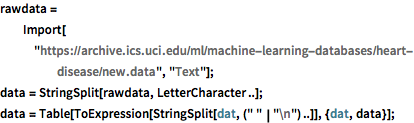
rawdata = Import["https://archive.ics.uci.edu/ml/machine-learning-databases/\ heart-disease/new.data", "Text"]; data = StringSplit[rawdata, LetterCharacter ..]; data = Table[ ToExpression[StringSplit[dat, (" " | "\n") ..]], {dat, data}];

Extrahieren Sie die relevanten Attribute in „Labels“ und „Features“. Die in „labels“ gespeicherten Werte sind 0 und 1, was jeweils dem Bestehen und der Abwesenheit einer Herzerkrankung entspricht.

In[2]:=

labels = Unitize[data[[All, 58]]]; features = data[[All, {3, 4, 9, 10, 12, 16, 19, 32, 38, 40, 41, 44, 51}]];

In[3]:=

Take[labels, 10]

Out[3]=

Für jeden Patienten ist der Feature-Vektor eine Liste numerischer Werte. Allerdings sind die Daten nicht vollständig und enthalten fehlende Felder, die als 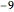gespeichert sind.

In[4]:=

features[[-3]]

Out[4]=

Ersetzen Sie fehlende Werte durch den Durchschnittswert der vorhandenen Daten im entsprechenden Attribut und visualisieren Sie dann die Korrelation zwischen verschiedenen Attributen.

In[5]:=

features = Transpose[Table[ N[attribute /. {-9 -> Mean[N[DeleteCases[attribute, -9]]]}] , {attribute, Transpose[features]}]]; cormat = Correlation[features];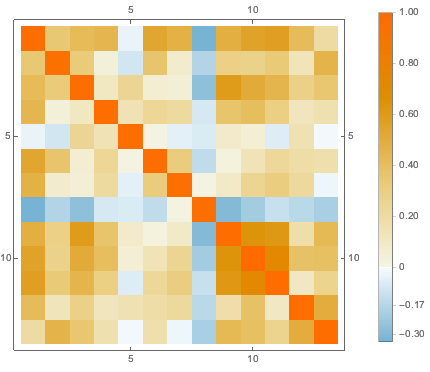

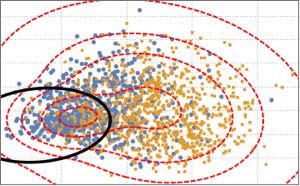
In[6]:=

MatrixPlot[cormat, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[6]=

Um die Datenverteilung zu veranschaulichen, wird eine Hauptkomponentenanalyse (PCA) durchgeführt, um die ersten beiden Hauptkomponenten zu extrahieren. Anschließend werden die projizierten Datenpunkte als Streudiagramm dargestellt.

In[7]:=

pcs2 = Take[PrincipalComponents[features, Method -> "Correlation"], All, 2];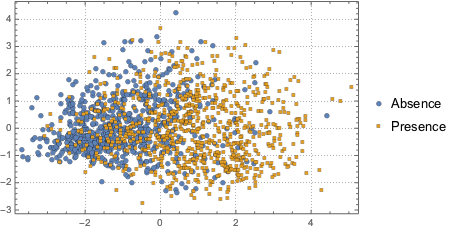

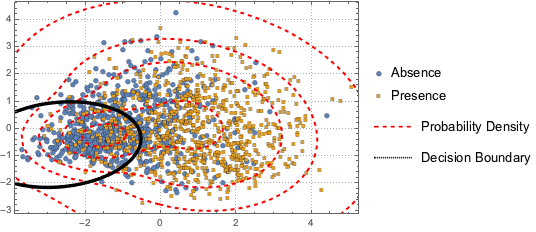
In[8]:=

splot = With[{ind = Pick[Range[Length[pcs2]], labels, 0]}, ListPlot[{pcs2[[ind]], Delete[pcs2, Transpose[{ind}]]}, ImageSize -> Medium, PlotTheme -> "Detailed", PlotMarkers -> Automatic, PlotLegends -> {"Absence", "Presence"}] ]

Out[8]=

Um die beiden Klassen voneinander zu trennen, werden die projizierten Daten einer Gaußschen Mischverteilung mit zwei Komponenten angepasst.

In[9]:=

edist = EstimatedDistribution[pcs2, MixtureDistribution[{p1, p2}, {BinormalDistribution[{m11, m12}, {s11, s12}, r1], BinormalDistribution[{m21, m22}, {s21, s22}, r2]}]];

Plotten Sie die Entscheidungsgrenze (schwarze Kurve) und die Konturen der Wahrscheinlichkeitsdichte (rote Kurve) der Mischverteilung und stellen Sie diese gemeinsam mit dem Streudiagramm dar. Die erste Komponente der Gaußschen Mischverteilung hat innerhalb der Entscheidungsgrenze eine höhere Wahrscheinlichkeit.

In[10]:=

Module[{p = edist[[1, 1]], dist1 = edist[[2, 1]], dist2 = edist[[2, 2]], prob}, prob[x_, y_] := p PDF[dist1, {x, y}]/(p PDF[dist1, {x, y}] + (1 - p) PDF[dist2, {x, y}]); Show[splot, ContourPlot[ PDF[edist, {x, y}] == {0.1, 0.05, 0.0125, 0.003, 0.0001}, {x, -4, 6}, {y, -4, 6}, ImageSize -> Medium, PlotTheme -> "Detailed", ContourStyle -> {Dashed, Thick, Red}, PlotLegends -> LineLegend[{Directive[Red, Dashed]}, {"Probability Density"}], PlotPoints -> 25], ContourPlot[prob[x, y] == 1/2, {x, -4, 6}, {y, -4, 6}, ImageSize -> Medium, PlotTheme -> "Detailed", ContourStyle -> {Thickness[.01], Black}, PlotLegends -> LineLegend[{Directive[Black, AbsoluteDashing[{1, 1}]]}, {"Decision Boundary"}], PlotPoints -> 25]] ]

Out[10]=