Wolfram Language™

Inhomogenener Poisson-Prozess

Ein inhomogener Poisson-Prozess ist ein Poisson-Prozess mit zeitvariaten Zuwächsen. Er kann zur Modellierung der Ankunft von Kunden in einem Geschäft, von Verkehrsereignissen und der Lage von Straßenschäden verwendet werden. Die Wahrscheinlichkeitsdichtefunktion des Prozesses zu allen Zeiten t entspricht einer Poisson-Verteilung.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]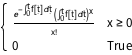

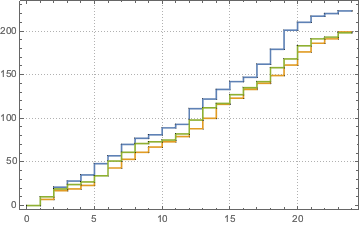
Out[1]=

Simulieren Sie einen inhomogenen Poisson-Prozess.

In[2]:=

td = RandomFunction[ InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];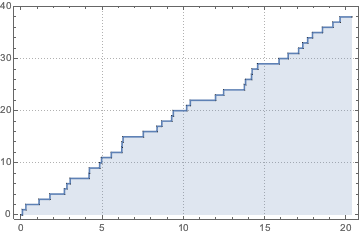

In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[3]=

Mit einem inhomogenen Poisson-Prozess kann man die Ankunft von Kunden modellieren. In diesem Beispiel wird mit dem Prozess die Ankunftszahl der Kunden in einem kleinem Fast-Food-Restaurant simuliert, wobei die stündlichen Kundenankunftspunkte gegeben sind.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 12}, {21, 6}, {22, 5}, {23, 7}}; \[Lambda][t_] = Interpolation[arrivalrates, InterpolationOrder -> 1][t];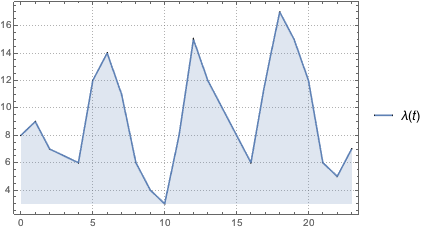

In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

Definieren Sie einen inhomogenen Poisson-Prozess für die Ankunftspunkte von Kunden basierend auf der angegebenen Intensitätsfunktion λ(t), und simulieren Sie Anzahl der Ankunftspunkte an einem Tag.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t]; td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=