WDF für Produkt/Quotienten von Zufallsvariablen
Ermitteln Sie die Wahrscheinlichkeitsdichtefunktion für das Verhältnis der kleinsten zur größten Stichprobe bei  unabhängigen Ziehungen einer BetaDistribution[2, 3].
unabhängigen Ziehungen einer BetaDistribution[2, 3].
In[1]:=

n = 5;
pdf = PDF[
TransformedDistribution[
min/max, {min, max} \[Distributed]
OrderDistribution[{BetaDistribution[2, 3], n}, {1, n}]], u]Out[1]=

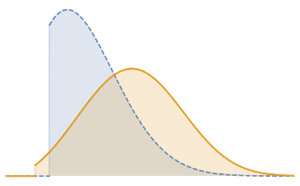
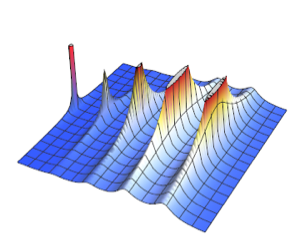
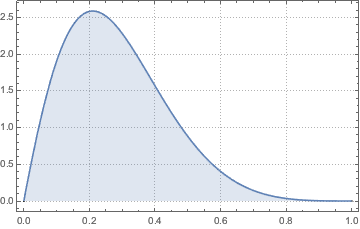
Visualisieren Sie die Dichte.
In[2]:=
Plot[pdf, {u, 0, 1}, PlotRange -> All, Filling -> Axis,
PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]Out[2]=
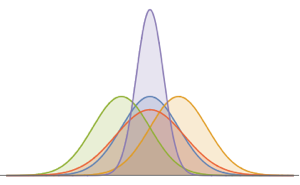
Berechnen Sie die Wahrscheinlichkeitsdichtefunktion des Produkts zweier Dreiecksverteilungen.
In[3]:=

pdf2 = PDF[
TransformedDistribution[
x1 x2, {x1 \[Distributed] TriangularDistribution[{-1, 2}, -1],
x2 \[Distributed] TriangularDistribution[{-4, 3}, 2]}], u]Out[3]=
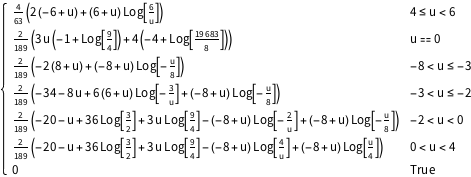
Den kompletten Wolfram Language-Input zeigen
Out[4]=
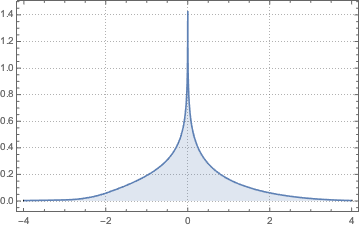
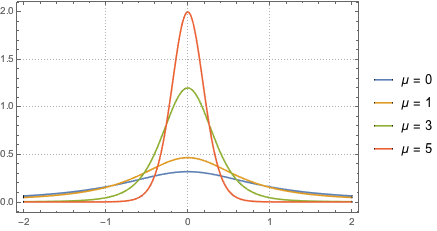
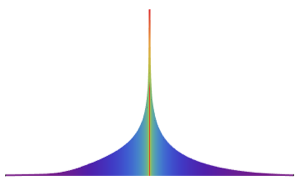
Ermitteln Sie die Wahrscheinlichkeitsdichtefunktion des Quotienten zweier unabhängiger normaler Zufallsvariablen.
In[5]:=

pdf3 = PDF[
TransformedDistribution[
z1/z2, {z1 \[Distributed] NormalDistribution[],
z2 \[Distributed] NormalDistribution[\[Mu], 1]}], x]Out[5]=
Die Verteilung ist endlastig bei jedem beliebigen fixen Wert von 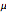 .
.
In[6]:=
Series[Exp[\[Mu]^2/2] pdf3, {x, Infinity, 8},
Assumptions -> \[Mu] > 0] // ExpandOut[6]=
Den kompletten Wolfram Language-Input zeigen
Out[7]=