Modellieren sozialer Netzwerke
Die verschobene Gompertz-Verteilung ist die Verteilung des Extremwerts unabhängiger exponentieller und extremwertig verteilter Zufallsvariablen. Die Verteilung eignet sich, um die Zu- und Abnahme von Interesse in sozialen Netzwerken zu berechnen. Die CDF (kumulative Verteilungsfunktion) der verschobenen Gompertz-Verteilung nimmt folgende Form an:
In[1]:=
CDF[ShiftedGompertzDistribution[\[Lambda], \[Xi]], x]Out[1]=
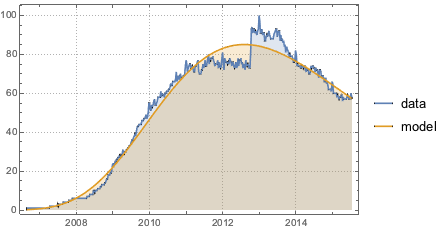
Wöchentliche Zählung des Interesses auf Facebook von Google Trends.
In[2]:=
ts = TemporalData[TimeSeries, {CompressedData["
1:eJyFz2tPwjAUBmDA+7wRNCpeQBTRiAGvXLoNYYytPW03QHSybiYav/tX/Ume
GRO/mPg0p+l72pykpbeP8VsmlUqlsT5xS/8n82smM/Nt9sdcYv4vC2gxoWlL
mqYto5WVVbS2tp7N5nK5jY3N7Z2tnXx+d3dvbx/XQbFwUCgUi4eHpdLRcbl8
UjmtnJ1XqxeoVqvV65dX9cvrZvP2pnHXaLUbjWaLIJMYuk4MwzTNTue+1+1a
qO9a9qA/cPq2PRg4ILnLgHPGgLkuABfSdRyHUs5AAghvyD3peb4U+IhLJoCB
NxLUk0JwgXcCRNIT2AYpPS4YByo5cGBsFL+oOFaRCqP4/VWpOFQqCKbhVEXh
9BmFKopjTFEQBs9PweRxNHkYj/yh7/ueEHI8xDGAg7AAqMsodRw3OTP2HWxK
XfyFbVl2z+p2kGn1jATRSZsQXW+RNkpSmxjkC/7xXxc=
"], {
TemporalData`DateSpecification[{2006, 8, 26, 0, 0, 0.}, {
2015, 7, 11, 0, 0, 0.}, {1, "Week"}]}, 1, {"Continuous", 1}, {
"Discrete", 1}, 1, {
ValueDimensions -> 1, DateFunction -> Automatic,
ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1}}},
True, 314.1];Den kompletten Wolfram Language-Input zeigen
Out[3]=
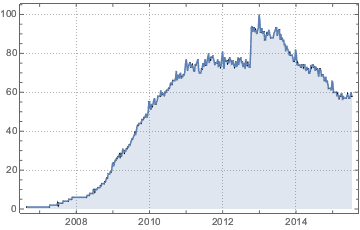
Die Daten werden einer verschobenen gestutzten Gompertz-Verteilung angepasst.
In[4]:=

rawcounts = ts["Values"];
length = Length[rawcounts];
x = Range[length] - 0.5;
wdata = WeightedData[x, rawcounts];In[5]:=

edist = EstimatedDistribution[wdata,
TruncatedDistribution[{0, length},
ShiftedGompertzDistribution[\[Lambda], \[Xi]]], {{\[Lambda],
1}, {\[Xi], 6}}]Out[5]=
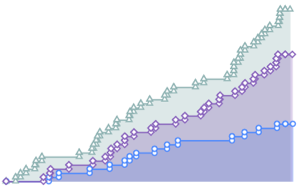
Vergleichen Sie die Prognosen des Modells mit den Daten.
Den kompletten Wolfram Language-Input zeigen
Out[6]=