Wolfram Language™

Umgang mit Unstetigkeiten in einer kumulativen Verteilungsfunktion

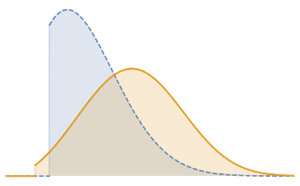
Definieren Sie eine formelbasierte Verteilung durch eine kumulative Verteilungsfunktion. Die Verteilungsfunktion enthält Sprungstellen, die eine Mischung aus kontinuierlichen und diskreten Komponenten sind.

In[1]:=

cdf = CDF[ MixtureDistribution[{1/3, 2/3}, {LaplaceDistribution[0, 1], TransformedDistribution[x - 2, x \[Distributed] BinomialDistribution[4, 1/3]]}], z];

In[2]:=

Plot[cdf, {z, -5, 5}, PlotTheme -> "Detailed", Filling -> Axis, ImageSize -> Medium, PlotLegends -> None]

Out[2]=

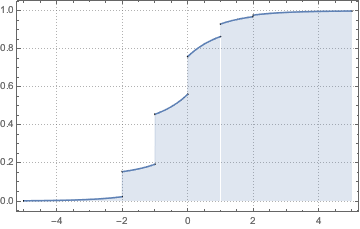
ProbabilityDistribution zerlegt die Verteilung in absolut kontinuierliche und diskrete Teile.

In[3]:=

ProbabilityDistribution[{CDF, cdf}, {z, -Infinity, Infinity}]

Out[3]=

Versehen Sie die WDF-Eingabe mit DiracDelta-Gewichtung.

In[4]:=

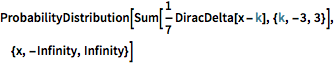
ProbabilityDistribution[ Sum[1/7 DiracDelta[x - k], {k, -3, 3}], {x, -Infinity, Infinity}]

Out[4]=