Wolfram Language™

Log-Returns von Aktienpreisen

Es wird angenommen, dass Log-Returns (Renditen) von Aktienpreisen, die mit einer geometrischen Brownschen Bewegung (im klassischen Black-Scholes-Modell) modelliert sind, normalverteilt sind. In diesem Beispiel wird diese Annahme anhand der Aktienpreise von fünf Unternehmen untersucht: Google, Microsoft, Facebook, Apple und Intel.

Rufen Sie die Aktienpreise des Jahres 2015 mit FinancialData ab.

In[1]:=

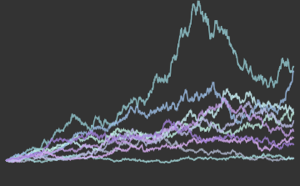
symbols = {"GOOGL", "MSFT", "FB", "AAPL", "INTC"}; prices = Table[ FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, symbols}];

Berechnen Sie die Log-Returns.

In[2]:=

logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

Filtern Sie die Log-Returns mit einem ARCHProcess erster Ordnung.

In[3]:=

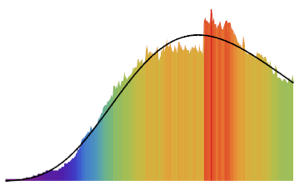
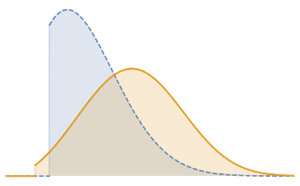
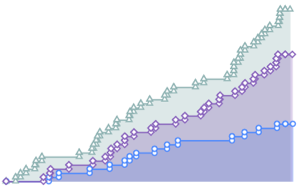
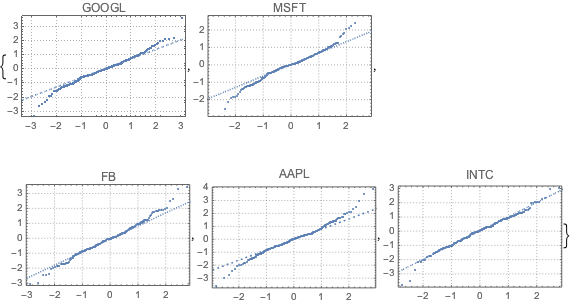
fdata = Table[ {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]]; MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2] , {lr, logreturn}]; fdata = Transpose[fdata];

Vergleichen Sie mithilfe von QuantilePlot die gefilterten Daten jeder Aktie mit der Normalverteilung. Die Renditen der Aktien aller fünf Unternehmen weichen an den Enden von der Normalverteilung ab.

In[4]:=

MapThread[ QuantilePlot[#1, PlotLabel -> #2, PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

Out[4]=

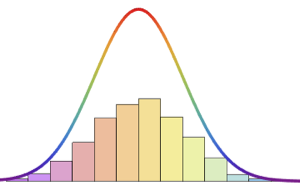
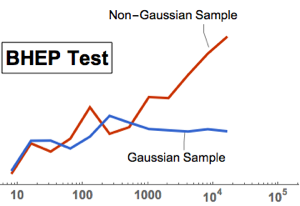
Führen Sie einen multivariaten Normalitätstest mit BaringhausHenzeTest (BHEP) durch. Die Hypothese einer Normalverteilung ist deutlich widerlegt.

In[5]:=

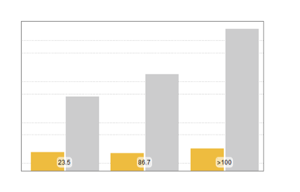
htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[6]:=

htd["TestDataTable"]

Out[6]=

In[7]:=

htd["ShortTestConclusion"]

Out[7]=

Passen Sie die gefilterten Daten mit MultinormalDistribution und MultivariateTDistribution an.

In[8]:=

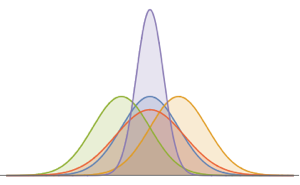
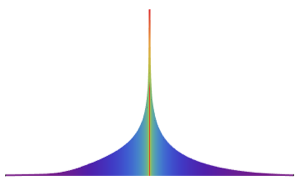
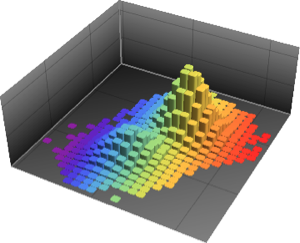
multiN = EstimatedDistribution[fdata, MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[8]=

In[9]:=

multiT = EstimatedDistribution[fdata, MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[9]=

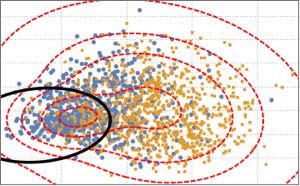
Berechnen Sie das Akaike-Informationskriterium (AIC) für die beiden Verteilungen. Das Modell der MultivariateTDistribution hat einen kleineren Wert.

In[10]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[11]:=

aic[5 + 15, multiN, fdata]

Out[11]=

In[12]:=

aic[5 + 15 + 1, multiT, fdata]

Out[12]=