‹›확장된 확률 및 통계 기능변환 된 분포의 자동 간략 기능
버전 11에서는 변환 된 분포의 자동 간략 규칙을 더 추가하였습니다.
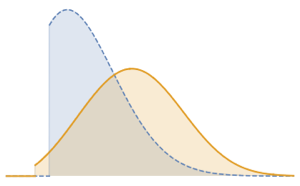
균일한 분포를 따르는 확률 변수의 힘은 베타 분포에 따릅니다.
TransformedDistribution[X^a, X \[Distributed] UniformDistribution[]]독립 지수 분포를 따르는 확률 변수의 비율은 파레토 분포를 만족합니다.
TransformedDistribution[
X/Y, {X \[Distributed] ExponentialDistribution[b],
Y \[Distributed] ExponentialDistribution[a]}]정규 분포를 따르는 확률 변수의 역수의 제곱은 레비 분포를 따릅니다.
TransformedDistribution[X^(-2),
X \[Distributed] NormalDistribution[0, s]]아래의 표에서 더많은 예를 찾아볼 수 있습니다.
전체 Wolfram 언어 입력 표시하기
SetAttributes[fun, HoldFirst];
fun[x_] := {HoldForm[x], x};
Grid[Map[Style[#, ScriptLevel -> 0] &,
Join[{{"Transformed Distribution", "Simplified Distribution"}}, {
fun[TransformedDistribution[
Min[Subscript[X, 1], Subscript[X,
2]], {Subscript[X, 1] \[Distributed]
BernoulliDistribution[Subscript[p, 1]],
Subscript[X, 2] \[Distributed]
BernoulliDistribution[Subscript[p, 2]]}]],
fun[TransformedDistribution[1/X,
X \[Distributed] LogLogisticDistribution[\[Gamma], \[Sigma]]]],
fun[TransformedDistribution[k*X,
X \[Distributed] ChiDistribution[\[Nu]]]],
fun[TransformedDistribution[1/X,
X \[Distributed] BetaPrimeDistribution[a, b]]],
fun[TransformedDistribution[k*Exp[-X],
X \[Distributed] ExponentialDistribution[a]]],
fun[TransformedDistribution[-Log[X],
X \[Distributed] PowerDistribution[1, a]]],
fun[TransformedDistribution[c*X,
X \[Distributed] ChiSquareDistribution[a]]],
fun[TransformedDistribution[1 + X,
X \[Distributed] ExponentialDistribution[a]]],
fun[TransformedDistribution[
Sqrt[X*Y], {X \[Distributed] ExponentialDistribution[m],
Y \[Distributed] GammaDistribution[a, b]}]],
fun[TransformedDistribution[Log[X]/2,
X \[Distributed] FRatioDistribution[n, m]]],
fun[TransformedDistribution[R^2,
R \[Distributed] RiceDistribution[\[Nu], 1]]]
}], {2}], Dividers -> All, Spacings -> {4, 2},
Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} ->
Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}},
BaseStyle -> {FontFamily -> Times, FontSize -> 13},
Alignment -> {Center, Center}] // TraditionalForm