비동차 푸아송 과정: Wolfram Language 11의 신기능

비동차 푸아송 과정

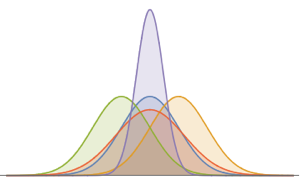
비동차 푸아송 과정은 시간에 따라 비율이 변동하는 푸아송 과정입니다. 이는 가게를 방문하는 고객의 도착 시간, 트래픽 이벤트, 도로의 손상 위치를 모델링하는데 사용할 수있습니다. 어떤 시간 슬라이스 t에서 가정의 확률 밀도 함수는 푸아송 분포를 따릅니다.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]

Out[1]=

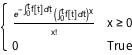
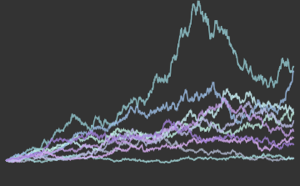
비동차 푸아송 과정의 시뮬레이션을 실시합니다.

In[2]:=

td = RandomFunction[
   InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];

전체 Wolfram 언어 입력 표시하기

In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, 
 PlotTheme -> "Detailed"]

Out[3]=

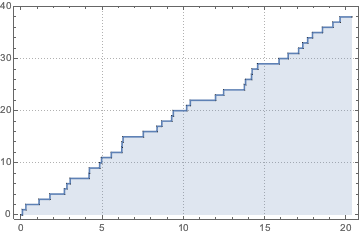
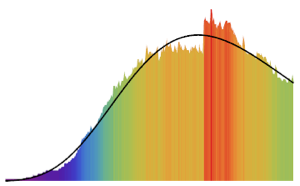
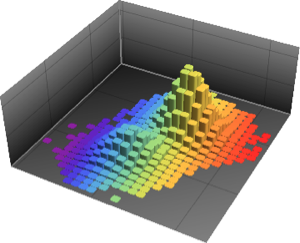
비동차 푸아송 과정은 도착 수를 모델링하는데 사용할 수있습니다. 여기에서는 이 과정을 작은 패스트푸드 레스토랑에서 시간당 고객의 도착 비율이 주어진 경우, 손님의 도착 수 시뮬레이션에 사용하였습니다.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 
    11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 
    10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 
    12}, {21, 6}, {22, 5}, {23, 7}};
\[Lambda][t_] = 
  Interpolation[arrivalrates, InterpolationOrder -> 1][t];

전체 Wolfram 언어 입력 표시하기

In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, 
 ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

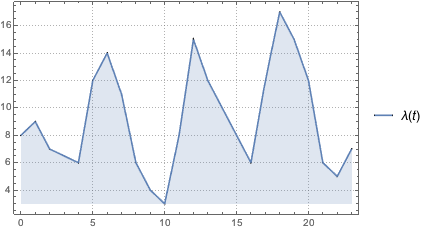
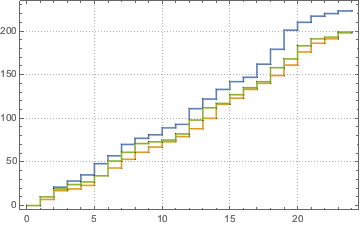
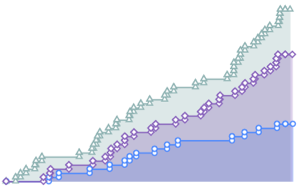
지정 비율 함수λ(t)에 근거하여 도착에 대한 비동차 푸아송 과정을 정의하고 1일내 도착 수를 시뮬레이션합니다.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t];
td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

전체 Wolfram 언어 입력 표시하기

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=

Wolfram 언어™

비동차 푸아송 과정

관련 예제