확률 변수의 곱과 몫의 확률 밀도 함수
BetaDistribution[2, 3]으로부터의  개의 독립적인 추출에서 최소부터 최대까지의 샘플 비율에 대한 확률 밀도 함수를 구합니다.
개의 독립적인 추출에서 최소부터 최대까지의 샘플 비율에 대한 확률 밀도 함수를 구합니다.
In[1]:=

n = 5;
pdf = PDF[
TransformedDistribution[
min/max, {min, max} \[Distributed]
OrderDistribution[{BetaDistribution[2, 3], n}, {1, n}]], u]Out[1]=

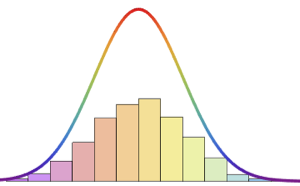
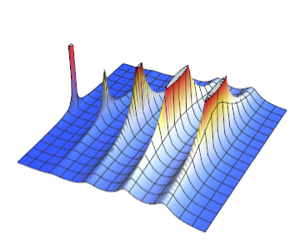
밀도를 시각화합니다.
In[2]:=
Plot[pdf, {u, 0, 1}, PlotRange -> All, Filling -> Axis,
PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]Out[2]=
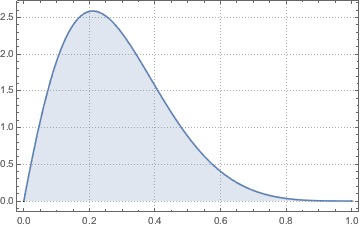
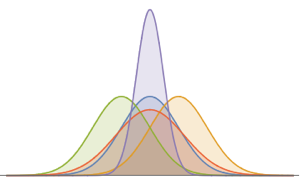
두개의 삼각형 분포의 곱에 대한 확률 밀도 함수를 계산합니다.
In[3]:=

pdf2 = PDF[
TransformedDistribution[
x1 x2, {x1 \[Distributed] TriangularDistribution[{-1, 2}, -1],
x2 \[Distributed] TriangularDistribution[{-4, 3}, 2]}], u]Out[3]=
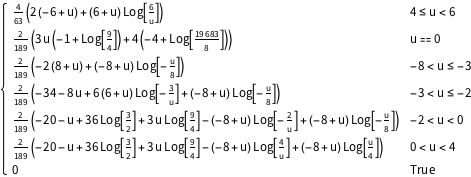
전체 Wolfram 언어 입력 표시하기
Out[4]=
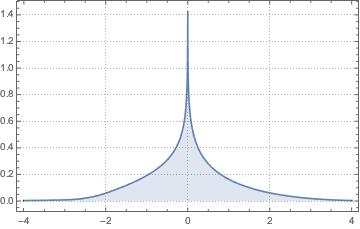
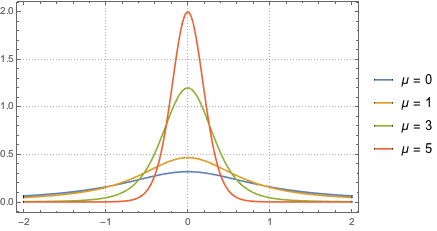
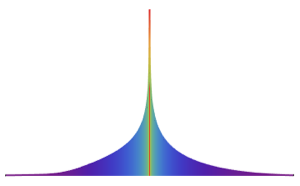
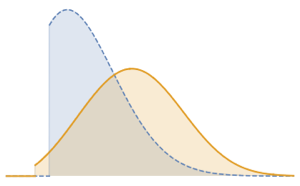
두개의 독립적인 정규 확률 변수의 몫에 대한 확률 밀도 함수를 구합니다.
In[5]:=

pdf3 = PDF[
TransformedDistribution[
z1/z2, {z1 \[Distributed] NormalDistribution[],
z2 \[Distributed] NormalDistribution[\[Mu], 1]}], x]Out[5]=
분포의 밑단은 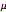 의 임의의 어떤 고정 값에 대해 무거워집니다.
의 임의의 어떤 고정 값에 대해 무거워집니다.
In[6]:=
Series[Exp[\[Mu]^2/2] pdf3, {x, Infinity, 8},
Assumptions -> \[Mu] > 0] // ExpandOut[6]=
전체 Wolfram 언어 입력 표시하기
Out[7]=