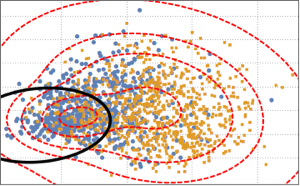
주가의 로그 수익률: Wolfram Language 11의 신기능

주가의 로그 수익률

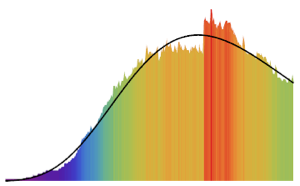
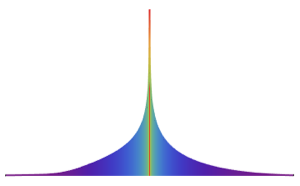
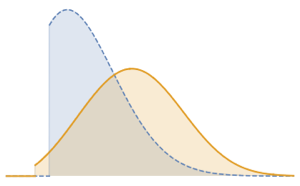
기하 브라운 운동 (고전적 블랙 숄즈 Black–Scholes 모델)에서 모델링 된 주가는 그 대수 이익률에서 정규 분포를 따른다고 가정합니다. 여기에서는 그 가정을 Google, Microsoft, Facebook, Apple, Intel의 5개 주가를 사용해 확인해봅니다.

FinancialData에서 2015년의 주가를 가져옵니다.

In[1]:=

symbols = {"GOOGL", "MSFT", "FB", "AAPL", "INTC"};
prices = Table[
   FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, 
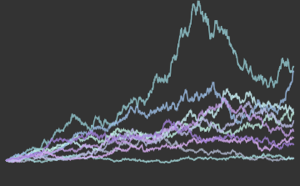
    symbols}];

로그 수익률을 계산합니다.

In[2]:=

logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

차수 1의 ARCHProcess에서 대수 이윤을 필터링합니다.

In[3]:=

fdata = Table[
   {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. 
     FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]];
   MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2]
   , {lr, logreturn}];
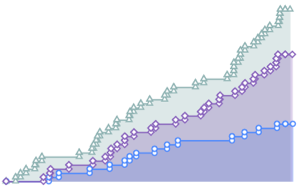
fdata = Transpose[fdata];

각 주에서 필터링 된 데이터와 정규 분포를 QuantilePlot을 사용하여 비교합니다. 5개 회사 모두에 대해 밑단 부분은 정규 분포에서 이탈합니다.

전체 Wolfram 언어 입력 표시하기

In[4]:=

MapThread[
 QuantilePlot[#1, PlotLabel -> #2, 
   PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

Out[4]=

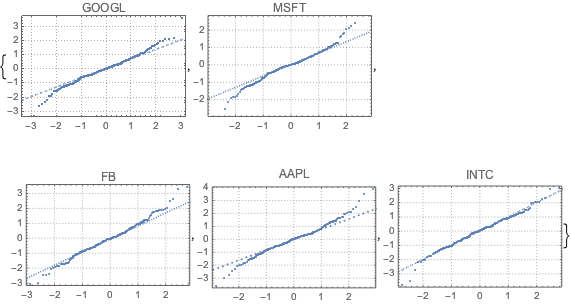
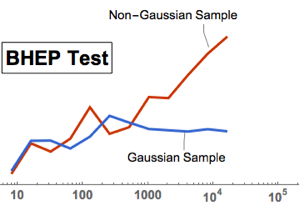
BaringhausHenzeTest (BHEP)을 사용하여 다변량의 정규성 검정을 실시합니다. 정규성 가정은 분명히 배척되고 있습니다.

In[5]:=

htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[6]:=

htd["TestDataTable"]

Out[6]=

In[7]:=

htd["ShortTestConclusion"]

Out[7]=

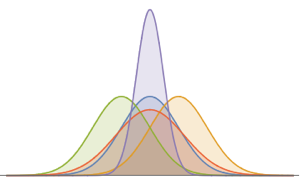
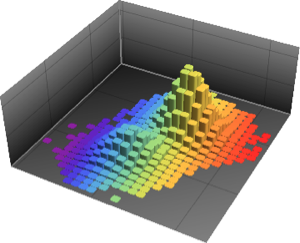
필터링 된 데이터를 MultinormalDistribution과 MultivariateTDistribution를 사용하여 피팅합니다.

In[8]:=

multiN = EstimatedDistribution[fdata, 
  MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[8]=

In[9]:=

multiT = EstimatedDistribution[fdata, 
  MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[9]=

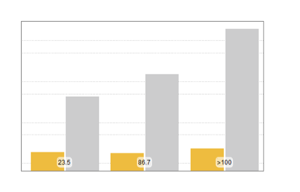
두개 분포의 아카이케 정보 기준 (AIC)을 계산합니다. MultivariateTDistribution 모델이 더 작은 값을 가집니다.

In[10]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[11]:=

aic[5 + 15, multiN, fdata]

Out[11]=

In[12]:=

aic[5 + 15 + 1, multiT, fdata]

Out[12]=

Wolfram 언어™

주가의 로그 수익률

관련 예제