Wolfram Language™

GPS-Empfänger und Höhe

GPS-Empfänger messen Standorte in Bezug auf ein abgeflachtes Referenzellipsoid, das die Oberfläche der Erde approximiert. In der Praxis jeodch sind berechnete Höhen mit dem Referenzellipsoid als Bezugssystem nicht ideal: So ist die Höhe der Oberfläche eines Sees in Bezug auf das Ellipsoid nicht konstant. Die Umwandlung in eine andere Bezugsfläche, das Geoid, welches den mittleren Meeresspiegel repräsentiert und diesen auch auf dem Land fortsetzt, ist also notwendig.

Die Abweichungen des Geoids von einem Referenzellipsoid werden Geoidundulation genannt. Downloaden Sie Undulationsdaten (angegeben in Fuß) für die zusammenhängenden Vereinigten Staaten.

In[1]:=

undulation = GeoElevationData[Entity["Country", "UnitedStates"], "Undulation"]

Out[1]=

Das Geoid ist immer unter dem Referenzellipsoid im Gebiet der USA.

In[2]:=

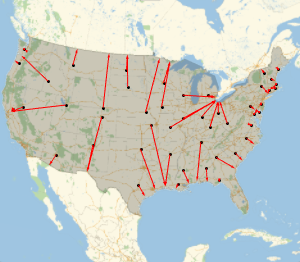
MinMax[undulation]

Out[2]=

Hier ist zum Beispiel die beobachtete Geoidundulation beim Wolfram Headquarters in Champaign.

In[3]:=

GeoElevationData[ GeoPosition[ Entity["City", {"Champaign", "Illinois", "UnitedStates"}]], "Undulation"]

Out[3]=

Downloaden Sie Daten für die ganze Welt.

In[4]:=

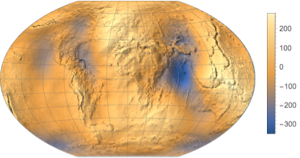
undulation = GeoElevationData["World", "Undulation"]

Out[4]=

Stellen Sie diese als eine Reliefkarte dar.

In[5]:=

image = ReliefPlot[undulation, DataReversed -> True, PlotRangePadding -> None, PlotLegends -> Automatic, MaxPlotPoints -> Infinity, Frame -> False]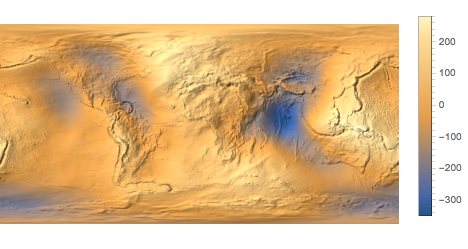

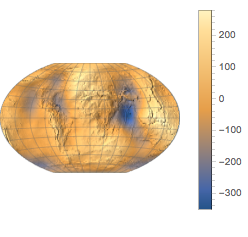
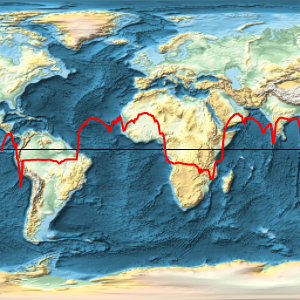
Out[5]=

Verwenden Sie eine andere Projektion.

In[6]:=

With[{bounds = {{-90, 90}, {-180, 180}}}, Legended[GeoGraphics[{GeoStyling[{"GeoImage", image[[1]]}, GeoRange -> bounds], GeoBoundsRegion[bounds]}, GeoRange -> bounds, GeoProjection -> "WinkelTripel", GeoGridLines -> True], image[[2]]]]

Out[6]=