Sphärische oder ellipsoide Mercator-Projektion

Die Mercator-Projektion erzeugt unterschiedliche Resultate, je nachdem, ob ein Kugelmodell oder ein Ellipsoidmodell der Erde verwendet wird. Die Wolfram Language ermöglicht es Ihnen, mit beiden Varianten zu arbeiten.

In[1]:=

webMercator = {"Mercator", "ReferenceModel" -> GeodesyData["WGS84", "SemimajorAxis"]}

Out[1]=

In[2]:=

ellipMercator = {"Mercator", "ReferenceModel" -> "WGS84"}

Out[2]=

Transformieren Sie den Standort der University of Oxford mit beiden Projektionen.

In[3]:=

p = GeoPosition[ Entity["University", "UniversityOfOxfordUnitedKingdom36022"]]

Out[3]=

In[4]:=

GeoGridPosition[p, webMercator][[1]]

Out[4]=

In[5]:=

GeoGridPosition[p, ellipMercator][[1]]

Out[5]=

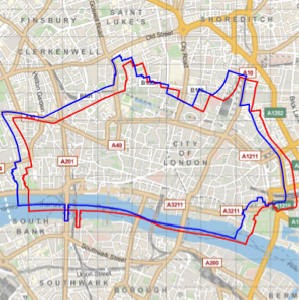
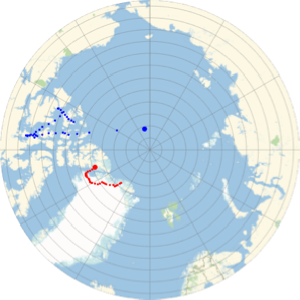
Es gibt eine vertikale Differenz, die auf der Karte mehr als 33 Kilometern entspricht.

In[6]:=

GeoGridPosition[p, webMercator][[1]]; GeoGridPosition[p, ellipMercator][[1]]; %% - %

Out[6]=

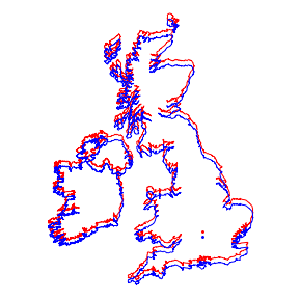
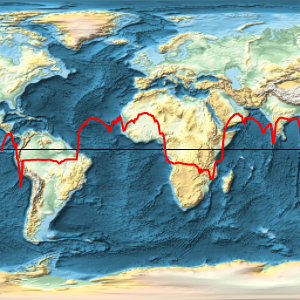
Erzeugen Sie Karten des Vereinigten Königreichs und Irlands auf Grundlage eines Kugel- und eines Ellipsoidmodells. Sie sehen fast identisch aus.

In[7]:=

webmap = GeoGraphics[{FaceForm[], EdgeForm[Red], Polygon[{Entity["Country", "UnitedKingdom"], Entity["Country", "Ireland"]}], Red, Point[p]}, GeoProjection -> webMercator, GeoBackground -> None][[1]]

Out[7]=

In[8]:=

ellipmap = GeoGraphics[{FaceForm[], EdgeForm[Blue], Polygon[{Entity["Country", "UnitedKingdom"], Entity["Country", "Ireland"]}], Blue, Point[p]}, GeoProjection -> ellipMercator, GeoBackground -> None][[1]]

Out[8]=

Wenn sie jedoch übereinandergelegt werden, sieht man den Unterschied ganz deutlich.

In[9]:=

Show[webmap, ellipmap]

Out[9]=