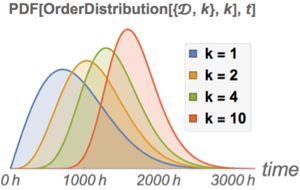
Distribuição truncada com medidas estatísticas

O diâmetro de uma cranberry americana segue uma distribuição normal com média de 16 mm e desvio padrão de 1.6 mm. A fruta precisa ter pelo menos 15 mm para ser vendida in natura; caso contrário, ela é usada para fazer molho de cranberry. Ache a distribuição do tamanho das frutas para serem vendidas in natura.

In[1]:=

cran\[ScriptCapitalD] = NormalDistribution[Quantity[16, "Millimeters"], Quantity[1.6, "Millimeters"]]; \[ScriptCapitalD] = TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]}, cran\[ScriptCapitalD]];

Compare as funções densidade de probabilidade.

In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]], PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22}, PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"}, Filling -> Axis, AxesLabel -> {"mm"}]

Out[2]=

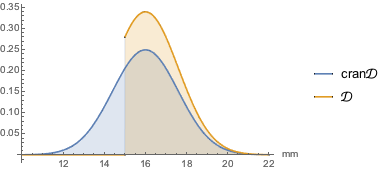
Supondo que um pacote de uma libra de cranberries tem um volume em torno de 30 in³, ache os limites da média inferior e superior para o número de cranberries deste pacote.

In[3]:=

lowerbound = Floor[NExpectation[ Divide[Quantity[30, "Inches"^3], Volume[Cuboid[{0, 0, 0}, {x, x, x}]]], x \[Distributed] \[ScriptCapitalD]]]

Out[3]=

In[4]:=

upperbound = Ceiling[NExpectation[ Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]], x \[Distributed] \[ScriptCapitalD]]]

Out[4]=