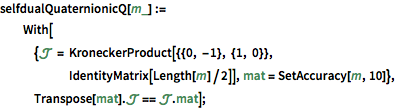원형 앙상블 (COE，CUE，...): Wolfram Language 11의 신기능

‹›

원형 앙상블 (COE，CUE，...)

원형 앙상블은 유니타리 행렬족으로, 분포는 다양한 유니타리 변환 아래에서 불변합니다. 이들은 주로 통계 역학, 정수론, 조합론, 원자 물리학 등에서 사용됩니다.

원형 실수 앙상블 (CRE)의 행렬은 직교 행렬입니다. »

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

원형 유니타리 앙상블 (CUE)의 행렬은 유니타리 행렬입니다. »

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

원형 직교 앙상블 (COE)의 행렬은 대칭 행렬이며 유니타리 행렬입니다. »

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

원형 심플랙틱 앙상블 (CSE)은 셀프 두얼 유니타리 쿼터니언 행렬입니다. »

전체 Wolfram 언어 입력 표시하기

In[7]:=

selfdualQuaternionicQ[m_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]],
     mat = SetAccuracy[m, 10]}, 
   Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

원형 쿼터니언 앙상블 (CQE)의 행렬은 심플랙틱 유니타리 행렬입니다. »

전체 Wolfram 언어 입력 표시하기

In[10]:=

symplecticMatrixQ[mat_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]]
    }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

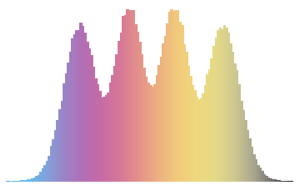
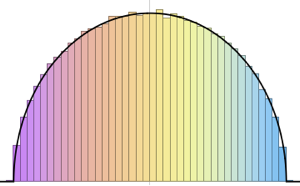
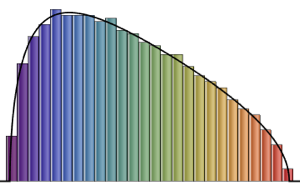
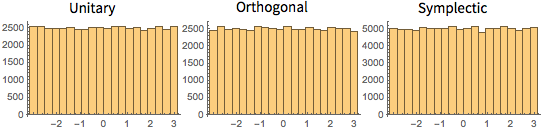
CUE, COE, CSE 행렬의 고유값은 단위 길이를 가지며 위상이 균등하게 분포하고있습니다.

전체 Wolfram 언어 입력 표시하기

In[13]:=

args = Flatten[
     Arg[RandomVariate[
       MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #],
        10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], 
    CircularOrthogonalMatrixDistribution[5], 
    CircularSymplecticMatrixDistribution[5]};
Row[MapThread[
  Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, 
    ChartLegends -> Placed[#2, Above]] &,
  {args, {Style["Unitary", 15], Style["Orthogonal", 15], 
    Style["Symplectic", 15]}}]]

Out[13]=

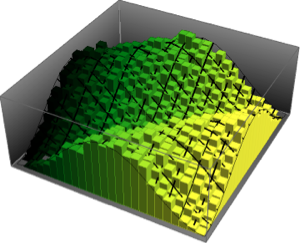
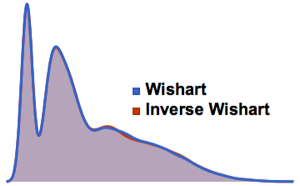
2차원 CUE의 고유값의 위상의 결합 분포를 시각화하고 실제 밀도와 비교합니다.

In[14]:=

evs\[ScriptCapitalD] = 
  MatrixPropertyDistribution[Arg[Eigenvalues[x]], 
   x \[Distributed] CircularUnitaryMatrixDistribution[2]];
\[CurlyPhi]s = 
  RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

전체 Wolfram 언어 입력 표시하기

In[14]:=

Show[
 Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, 
  PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"],
 Plot3D[1/(8 Pi^2)
    Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, 
   Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], 
 ImageSize -> Medium]

Out[15]=

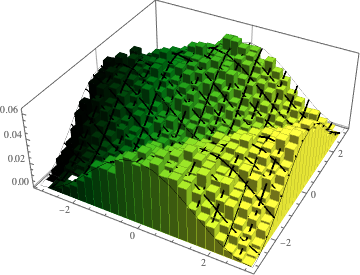
전체 Wolfram 언어 입력 표시하기

In[16]:=

Show[
 Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, 
  ChartStyle -> "AvocadoColors"],
 Plot3D[1/(8 Pi^2)
    Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, 
   Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick, 
  PlotTheme -> "Marketing"], ImageSize -> Medium, Axes -> False]

Wolfram 언어™

원형 앙상블 (COE，CUE，...)

관련 예제