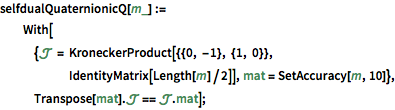Wolfram Language™

Ensembles circulaires (COE, CUE...)

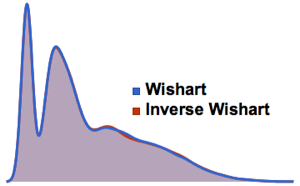
Les ensembles circulaires sont des familles de matrices unitaires dont les lois sont invariantes sous l'effet de différentes transformations unitaires. Les applications typiques sont la mécanique statistique, la théorie des nombres, la combinatoire et la physique nucléaire.

Les matrices d'un ensemble circulaire (CRE) sont orthogonales. »

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

Les matrices circulaires de l'ensemble unitaire (CUE) sont unitaires. »

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

Les matrices circulaires de l'ensemble orthogonal (COE) sont symétriques et unitaires. »

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

Les matrices d'un ensemble symplectique circulaire (CSE) sont quaternioniques unitaires auto-duales. »

In[7]:=

selfdualQuaternionicQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]], mat = SetAccuracy[m, 10]}, Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

Les matrices de l'ensemble de quaternions circulaires (CQE) sont unitaires symplectiques. »

In[10]:=

symplecticMatrixQ[mat_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]] }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

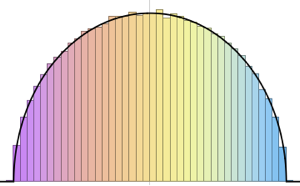
cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

Les valeurs propres des matrices de CUE, COE et CSE ont une longueur unitaire et sont uniformément distribuées en phase.

In[13]:=

args = Flatten[ Arg[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], CircularOrthogonalMatrixDistribution[5], CircularSymplecticMatrixDistribution[5]}; Row[MapThread[ Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, ChartLegends -> Placed[#2, Above]] &, {args, {Style["Unitary", 15], Style["Orthogonal", 15], Style["Symplectic", 15]}}]]

Out[13]=

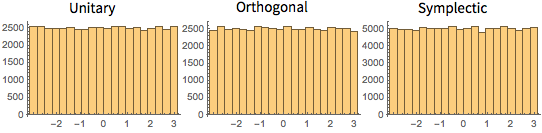
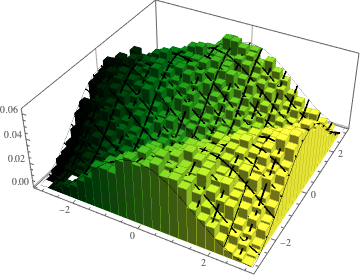
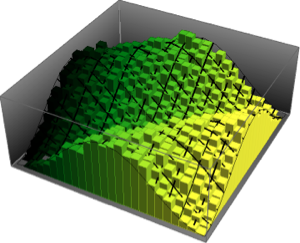
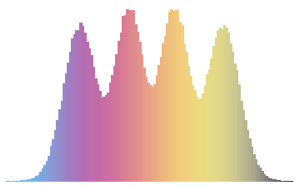
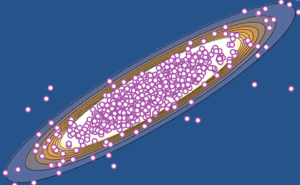
Visualisez la loi conjointe de la phase des valeurs propres à deux dimensions d'une CUE et comparez-la avec la densité actuelle.

In[14]:=

evs\[ScriptCapitalD] = MatrixPropertyDistribution[Arg[Eigenvalues[x]], x \[Distributed] CircularUnitaryMatrixDistribution[2]]; \[CurlyPhi]s = RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

In[14]:=

Show[ Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"], Plot3D[1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], ImageSize -> Medium]

Out[15]=