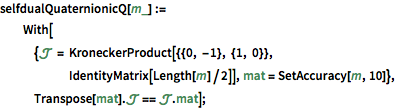Круговые ансамбли (КОА, КУА,...)

Круговые ансамбли - это семейства унитарных матриц с неизменными распределениями при различных унитарных трансформациях. Их обычно применяют в статистической механике, теории чисел, комбинаторике и ядерной физике.

Матрицы из кругового действительного ансамбля (КДА) являются ортогональными. »

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

Матрицы из кругового унитарного ансамбля (КУА) являются унитарными. »

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

Матрицы из кругового ортогонального ансамбля (КОА) являются симметричными и унитарными. »

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

Матрицы из кругового симплектического ансамбля (КСА) являются автодуальными унитарными кватернионными. »

In[7]:=

selfdualQuaternionicQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]], mat = SetAccuracy[m, 10]}, Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

Матрицы из кругового кватернионного ансамбля (ККА) являются симплектическими унитарными. »

In[10]:=

symplecticMatrixQ[mat_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]] }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

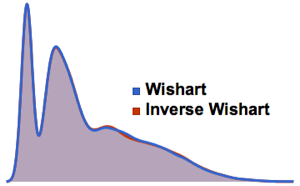
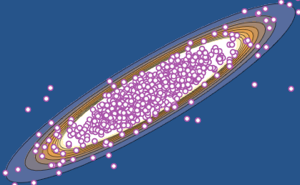
cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

Собственные значения матриц из КУА, КОА и КСА имеют равные единицы длины и равномерно распределены по фазе.

In[13]:=

args = Flatten[ Arg[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], CircularOrthogonalMatrixDistribution[5], CircularSymplecticMatrixDistribution[5]}; Row[MapThread[ Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, ChartLegends -> Placed[#2, Above]] &, {args, {Style["Unitary", 15], Style["Orthogonal", 15], Style["Symplectic", 15]}}]]

Out[13]=

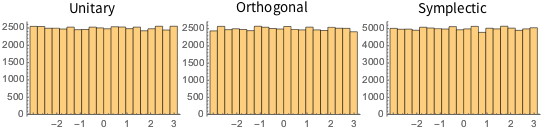
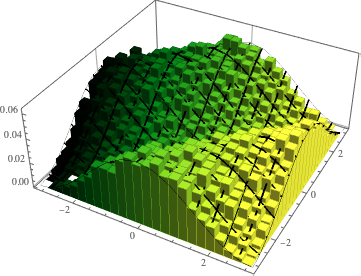
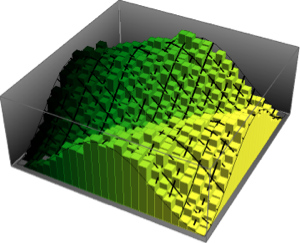
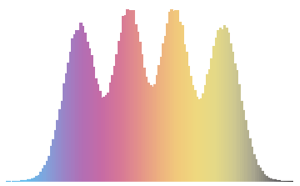
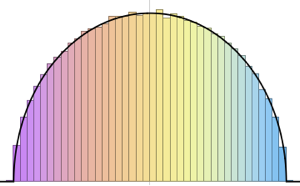
Визуализируйте совместное распределение фазы собственных значений из двухмерного КУА и сравните его с фактической плотностью.

In[14]:=

evs\[ScriptCapitalD] = MatrixPropertyDistribution[Arg[Eigenvalues[x]], x \[Distributed] CircularUnitaryMatrixDistribution[2]]; \[CurlyPhi]s = RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

In[14]:=

Show[ Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"], Plot3D[1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], ImageSize -> Medium]

Out[15]=