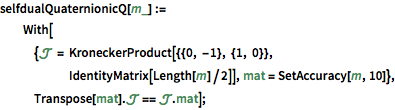圆环系综（COE、CUE、...）: Wolfram语言 11 的新功能

‹›

圆环系综（COE、CUE、...）

圆环系综是在不同酉变换下分布不变的酉矩阵家族. 典型应用于统计力学、数论、组合数学和核物理学中.

由圆环实系综（CRE）得到的矩阵是正交矩阵. »

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

由圆环酉系综（CUE）得到的矩阵是酉矩阵. »

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

由圆环正交系综（COE）得到的矩阵是对称的酉矩阵. »

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

由圆环辛系综（CSE）得到的矩阵是自对偶四元数酉矩阵. »

显示完整的 Wolfram 语言输入

In[7]:=

selfdualQuaternionicQ[m_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]],
     mat = SetAccuracy[m, 10]}, 
   Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

由圆环四元数系综 (CQE) 得到的矩阵是辛酉矩阵. »

显示完整的 Wolfram 语言输入

In[10]:=

symplecticMatrixQ[mat_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]]
    }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

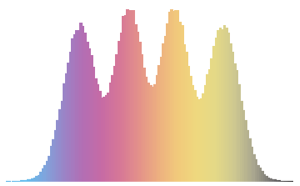
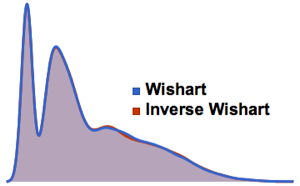
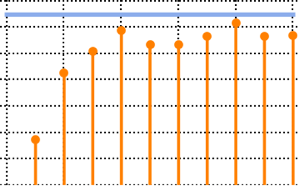
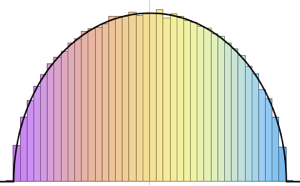
由 CUE、COE 和 CSE 得到的矩阵特征值具有单位长度并且在相位上均匀分布.

显示完整的 Wolfram 语言输入

In[13]:=

args = Flatten[
     Arg[RandomVariate[
       MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #],
        10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], 
    CircularOrthogonalMatrixDistribution[5], 
    CircularSymplecticMatrixDistribution[5]};
Row[MapThread[
  Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, 
    ChartLegends -> Placed[#2, Above]] &,
  {args, {Style["Unitary", 15], Style["Orthogonal", 15], 
    Style["Symplectic", 15]}}]]

Out[13]=

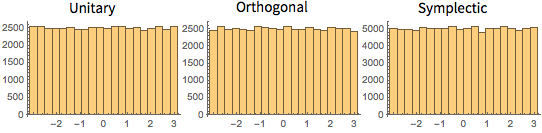
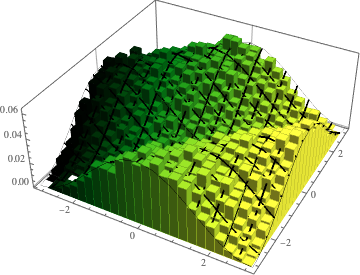
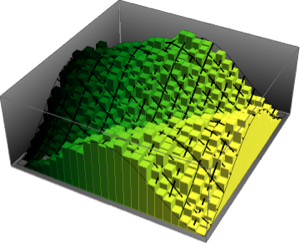
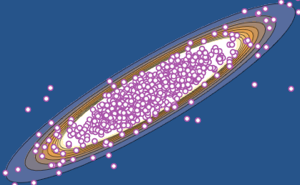
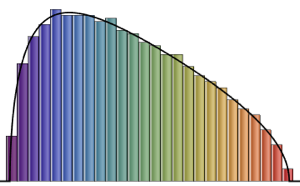
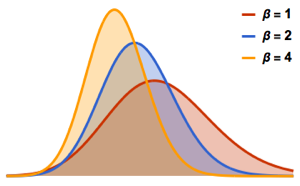
对来自二维 CUE 的特征值相位联合分布进行可视化，并将其与实际密度比较.

In[14]:=

evs\[ScriptCapitalD] = 
  MatrixPropertyDistribution[Arg[Eigenvalues[x]], 
   x \[Distributed] CircularUnitaryMatrixDistribution[2]];
\[CurlyPhi]s = 
  RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

显示完整的 Wolfram 语言输入

In[14]:=

Show[
 Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, 
  PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"],
 Plot3D[1/(8 Pi^2)
    Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, 
   Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], 
 ImageSize -> Medium]

Out[15]=

Wolfram 语言™

圆环系综（COE、CUE、...）

相关范例