Wolfram Language™

Subsequências crescentes mais longas

O número de permutações 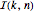de elementos 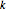onde a subsequência crescente mais longa está na maior parte da longitude , pode ser calculado fazendo uma média sobre 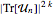, onde 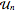são matrizes extraídas de CircularUnitaryMatrixDistribution de dimensão .

In[1]:=

{k, n} = {6, 2};

Defina a distribuição de propriedades de matriz e calcule a média.

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

Compare com a contagem direta.

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

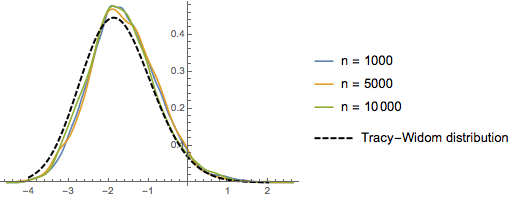
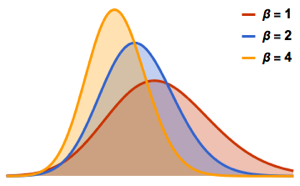
Para 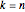,a distribuição dos comprimentos escalados das maiores subsequências crescentes de permutações aleatórias converge com a distribuição Tracy-Widom com .

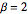In[4]:=

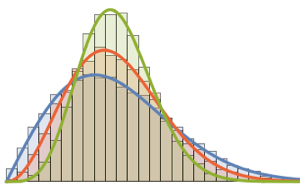
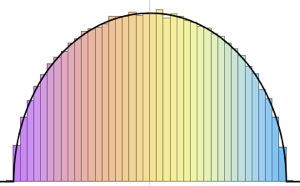
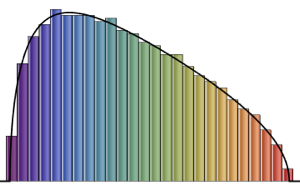
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

Compare o histograma alisado de comprimentos escalados da amostra para aumentar as dimensões com a função densidade de probabilidade da distribuição de Tracy-Widom.

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=