最長増加部分列

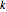最長増加部分列が最大で長さ である 個の元の置換数 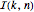は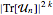，を平均することで計算できる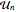．はCircularUnitaryMatrixDistributionから導かれた次元 の行列である．

In[1]:=

{k, n} = {6, 2};

行列の特性分布を定義し，平均を計算する．

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

直接の数と比較する．

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

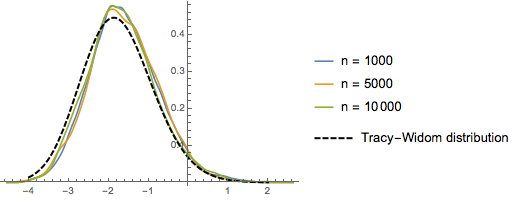
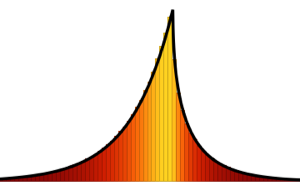
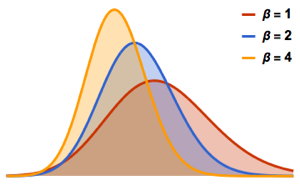
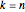のとき，ランダム置換の最長増加部分列のスケールされた長さの分布は 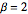のトレーシー・ウィダム分布に収束する．

In[4]:=

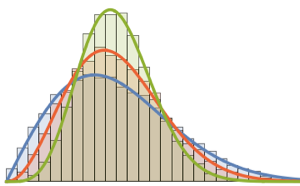
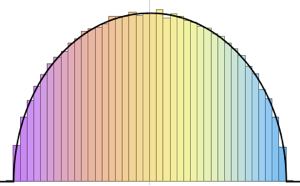
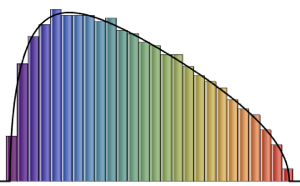
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

大きくなる次元についてサンプルとして取られたスケールされた長さの滑らかなヒストグラムをトレーシー・ウィダム分布の確率密度関数と比較する．

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=