Subsecuencias crecientes más largas

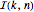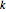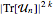El número de permutaciones de elementos en donde la subsecuencia creciente más larga está en la mayor parte de la longitud , puede ser calculada promediando , donde 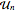son matrices extraídas de CircularUnitaryMatrixDistribution de dimensión .

In[1]:=

{k, n} = {6, 2};

Defina la distribución de propiedades de matriz y calcule la media.

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

Compare con el conteo directo.

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

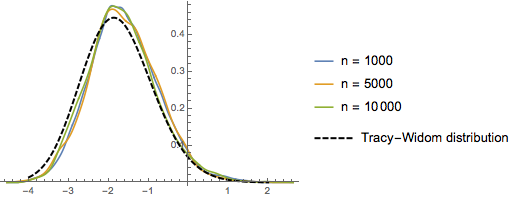
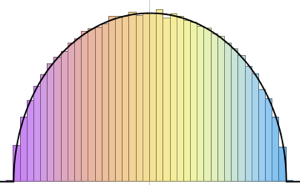
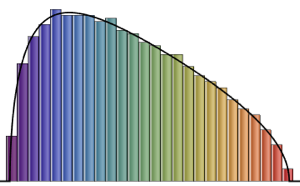
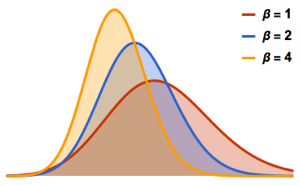
Para 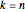, la distribución de las longitudes escaladas de subsecuencias crecientes más grandes de permutaciones aleatorias converge con la distribución Tracy–Widom con .

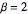In[4]:=

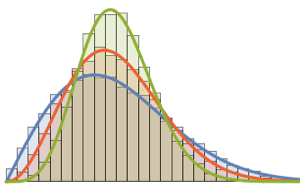
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

Compare el histograma alisado de longitudes escaladas muestreadas para aumentar las dimensiones con la función de densidad de probabilidad de la distribución de Tracy–Widom.

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=