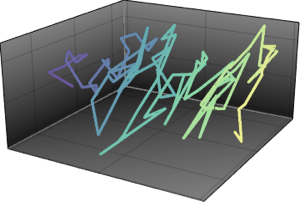
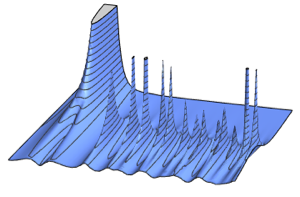
最长增长子序列

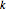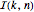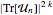对于含 个元素的排列 ，它的最长增长子序列的长度最多为 ，其排列数可以通过在 上取平均计算，其中 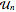是从维度为 的 CircularUnitaryMatrixDistribution 中抽取的矩阵.

In[1]:=

{k, n} = {6, 2};

定义矩阵属性分布，并计算均值.

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

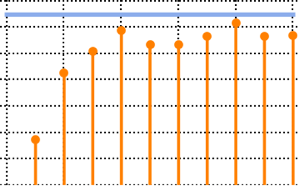
与直接计数比较.

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

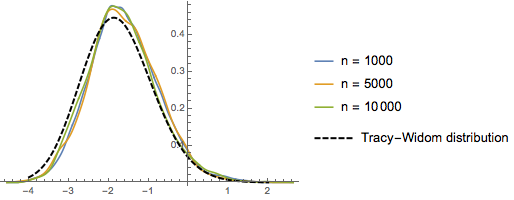
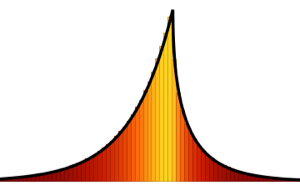
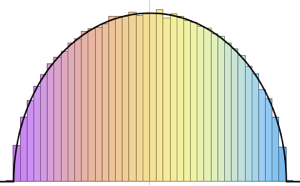
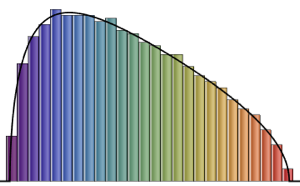
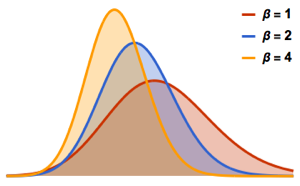
对于 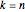，随机排列的最长增长子序列的缩放长度分布收敛于 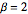的特雷西–维多姆分布.

In[4]:=

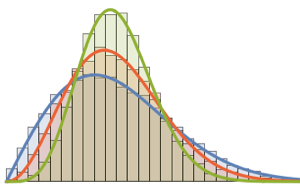
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

将维数增加的缩放长度采样的平滑直方图与特雷西–维多姆分布的概率密度函数比较.

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=