Sous-séquences croissantes les plus longues

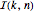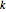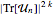Le nombre de permutations d'éléments dans lesquels la sous-séquence croissante la plus longue se trouve dans la partie de la longueur , peut être calculée au moyen de , où 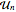sont des matrices extraites de CircularUnitaryMatrixDistribution de dimension .

In[1]:=

{k, n} = {6, 2};

Définissez la distribution de propriétés de la matrice et calculez la moyenne.

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

Comparez avec le comptage direct.

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

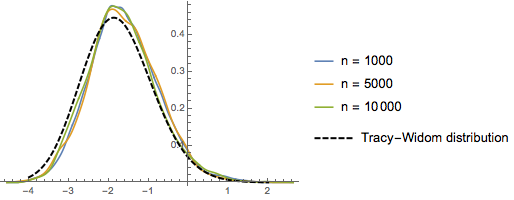
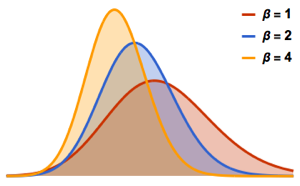
Pour 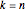,la distribution des longueurs échelonnées des plus longues sous-séquences croissantes de permutations aléatoires converge vers la loi de Tracy–Widom .

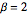In[4]:=

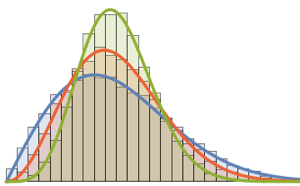
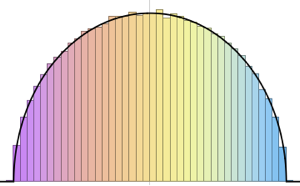
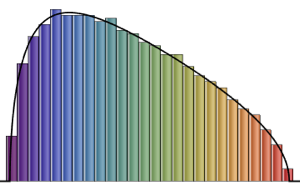
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

Comparez l'histogramme lisse de longueurs d'échelle échantillonnées pour augmenter les dimensions avec la fonction de densité de probabilité de la loi de Tracy–Widom.

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=