Wolfram Language™

EntityStore für Integraltransformationen

Eine Integraltransformation ist eine mathematische Operation, die eine Funktion 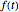auf eine andere 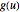mithilfe der Vorschrift 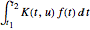abbildet, wobei 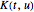der Kern ist. Integraltransformationen sind sehr wichtig in vielen Bereichen wie der Signalverarbeitung, in der medizinischen Bildgebung und der Wahrscheinlichkeitstheorie. In diesem Beispiel illustrieren wir das Anlegen eines Entity-Stores mit Eigenschaften wichtiger Transformationen.

Der Entity-Store kann manuell codiert werden, indem Sie die wichtigsten Eigenschaften von Integraltransformationen in einer EntityStore-Datenstruktur notieren.

In[1]:=

EntityStore[<| "Types" -> <| "IntegralTransform" -> <| "Entities" -> <| "ExponentialFourierTransform" -> <| "Label" -> "exponential Fourier transform", "StandardName" -> "ExponentialFourierTransform", "StandardNotation" -> Hold[f[t]], "Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[Integrate][ E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[ 2 \[Pi]], "GeneralProperties" -> <| "Linearity" -> {Inactive[FourierTransform][ a f[t] + b g[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) a Inactive[FourierTransform][f[t], t, z] + b Inactive[FourierTransform][g[t], t, z], Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] + Inactive[FourierTransform][f[t] UnitStep[t], t, z]}, "Reflection" -> {Inactive[FourierTransform][f[-t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]}, "Dilation" -> {ConditionalExpression[ Inactive[FourierTransform][f[a t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals && a \!\(\* TagBox["!=", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!="]\) 0]}, "Shifting or translation" -> {ConditionalExpression[ Inactive[FourierTransform][f[-a + t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]

Out[1]=

Eine komplettere Version können Sie aus folgendem CloudObject abrufen.

In[2]:=

itstore = CloudGet[CloudObject[ "https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\ 5088f435fe99"]]

Out[2]=

Registrieren Sie den Store für diese Sitzung.

In[3]:=

PrependTo[$EntityStores, itstore];

Sehen Sie sich die Entitäten im Store an.

In[4]:=

EntityValue["IntegralTransform", "Entities"]

Out[4]=

Fügen Sie eine neue Transformation hinzu.

In[5]:=

Entity["IntegralTransform", "HilbertTransform"]["Label"] = "Hilbert transform"; Entity["IntegralTransform", "HilbertTransform"]["Definition"] = Inactive[HilbertTransform][f[t], t, x] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) 1/\[Pi] Inactive[Integrate][f[t]/( t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True, Assumptions -> x \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals];

Geben Sie die derzeit verfügbaren Eigenschaften für Integraltransformationen zurück.

In[6]:=

EntityValue["IntegralTransform", "Properties"]

Out[6]=

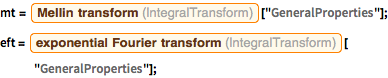
Rufen Sie die Definitionen für exponentielle Fourier- und Mellin-Transformationen ab.

In[7]:=

EntityValue[ Entity["IntegralTransform", "LaplaceTransform"], "Definition"]

Out[7]=

In[8]:=

EntityValue[ Entity["IntegralTransform", "MellinTransform"], "Definition"]

Out[8]=

Vergleichen Sie diese mit dem Ergebnis der eingebauten Funktion.

In[9]:=

Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"], "Definition"][[2]] /. f :> Function[t, ArcTan[t]]]

Out[9]=

In[10]:=

LaplaceTransform[ArcTan[t], t, z]

Out[10]=

Zeigen Sie die Faltung der Z-Transformation an.

In[11]:=

Entity["IntegralTransform", "ZTransform"][ "GeneralProperties"]["Convolution"]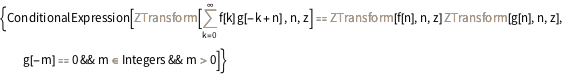

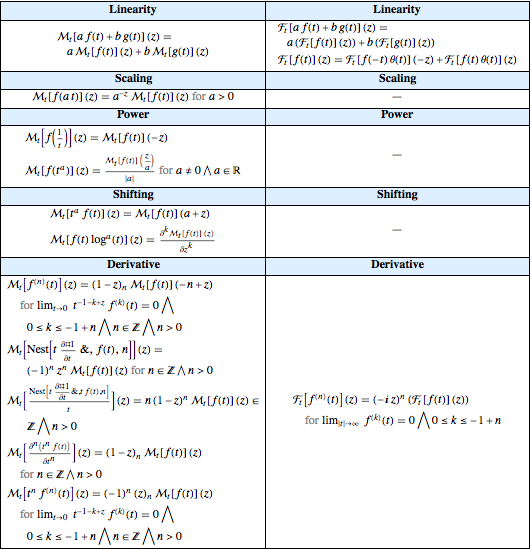
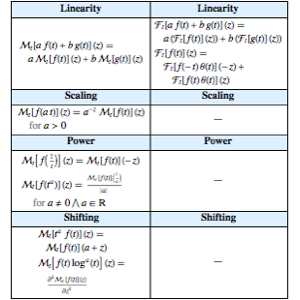
Out[11]=

Vergleichen Sie die derzeit gespeicherten Eigenschaften der exponentiellen Fourier- und Mellin-Transformationen.

In[12]:=

format[l_] := If[MatchQ[l, _Missing], "\[LongDash]", Activate[HoldForm @@ ({Column[l]} /. HoldPattern[ConditionalExpression[a_, b_]] :> Row[{a, Style[ " for ", Gray], b}])]]

In[13]:=

mt = Entity["IntegralTransform", "MellinTransform"][ "GeneralProperties"]; eft = Entity["IntegralTransform", "ExponentialFourierTransform"][ "GeneralProperties"];

In[14]:=

Grid[Take[ Flatten[{{Style[#, Bold], Style[#, Bold]}, {format@mt[#], format@eft[#]}} & /@ DeleteDuplicates[Join[Keys[mt], Keys[eft]]], 1], 10], Dividers -> All, Background -> {None, {{LightBlue, White}}}] // TraditionalForm

Out[14]//TraditionalForm=