Ermitteln Sie den Wert eines Sacks Münzen: Neu in Wolfram Language 11

Ermitteln Sie den Wert eines Sacks Münzen

Ein 1 Pfund schwerer Sack voll neuer US-amerikanischer Münzen wird aus einer Bank gestohlen. Was kann man, ohne den Sack zu öffnen, über dessen Geldwert aussagen? Eine offensichtliche und leicht zu messende Charakteristik ist das Gewicht des Sackes. Kombinieren Sie unter der Annahme eines Sack Münzen mit dem Gewicht eines Pfunds das Währungswissen der Wolfram Knowledgebase und die eingebaute Fähigkeit zur Lösung linearer Gleichungen, um den Erwartungswert des erbeuteten Geldsacks zu berechnen.

Ermitteln Sie als ersten Schritt eine Liste der sich derzeit im Umlauf befindenden US-amerikanischen Münzen.

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[
    "CurrencyDenomination", "IssuingCountry"] -> 
   Entity["Country", "UnitedStates"], 
  EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

Erweitern Sie die implizit definierte Entitätsklasse, indem Sie auf [+] klicken, finden Sie deren Mitglieder und sortieren Sie diese nach Wert.

In[2]:=

coinsUS = EntityList[
EntityClass[
   "CurrencyDenomination", {
    EntityProperty[
      "CurrencyDenomination", "IssuingCountry"] -> Entity[
      "Country", "UnitedStates"], 
     EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // 
  SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

Erstellen Sie eine Collage von Münzenbildern.

In[3]:=

ImageCollage[
 EntityValue[coinsUS, 
  EntityProperty["CurrencyDenomination", "Image"]], 
 Background -> White]

Out[3]=

Fassen Sie die Münzeigenschaften in einer Tabelle zusammen.

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, 
     Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ 
   EntityValue[
    coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], 
     EntityProperty["CurrencyDenomination", "Image"], 
     EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], 
  Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm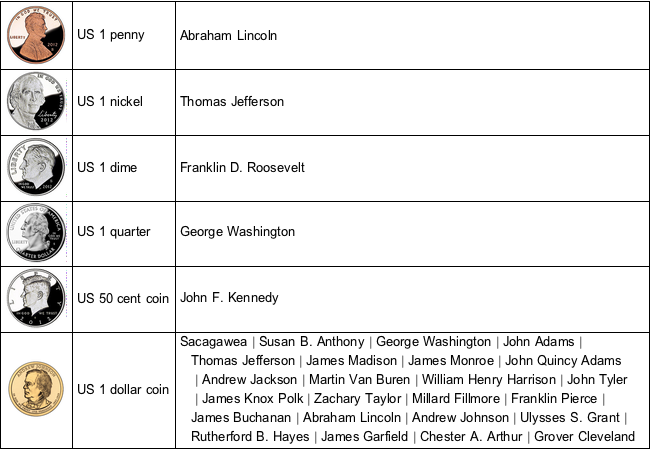

Out[4]//TraditionalForm=

Ermitteln Sie die Münzbezeichnungen (in Cents) und die jeweilige Masse (in Gramm) und konvertieren Sie die Massewerte in rationale Zahlen.

In[5]:=

{values, masses} = 
 Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{
   QuantityMagnitude[UnitConvert[values, "USCents"]],
   Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]]
   }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

Ermitteln Sie alle Münzverteilungen, die mit einem Gewicht von 1 Pfund (Messfehler von ± 0.1%) kompatibel sind (unter der Annahme, dass das Eigengewicht des Sacks vernachlässigbar gering ist).

In[9]:=

meanWeight = 
  QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, 
  maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], 
  Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

Bestimmen Sie mit FrobeniusSolve alle möglichen Münzkombinationen, die das gefragte Gesamtgewicht ergeben.

Den kompletten Wolfram Language-Input zeigen

In[12]:=

allSolutions = Monitor[
   Table[fb = 
     FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight,
      minScaledWeight, maxScaledWeight}],
   Row[{NumberForm[
      100. (scaledweight - minScaledWeight)/(maxScaledWeight - 
          minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], 
     "%: ", Length[fb], " solutions"}]
   ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

Ermitteln Sie den Mindest-, Median, Median- und Maximalwert des Gesamtwerts der Münzen im Sack (unter der Annahme, dass alle Kombinationen gleich wahrscheinlich sind).

Den kompletten Wolfram Language-Input zeigen

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, 
   Transpose[{stats, 
     NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ 
      Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}},
   Dividers -> All, 
  Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

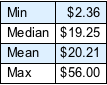
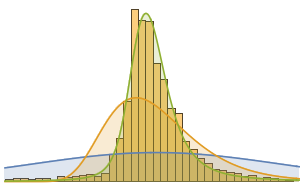
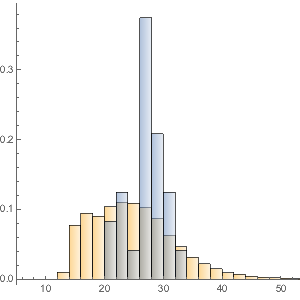
Erstellen Sie ein Histogramm der Verteilung des Gesamtgeldwerts.

In[17]:=

Histogram[dollarValues, Automatic, "PDF", 
 AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]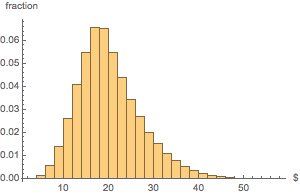

Out[17]=

Die Gewichtsverteilung aller Säcke ist ziemlich einheitlich.

Den kompletten Wolfram Language-Input zeigen

In[18]:=

weights = coinsandweights[[All, -1]];
lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];
weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", 
 AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]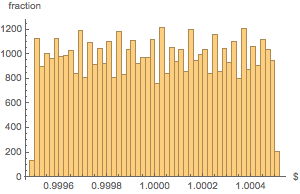

Out[19]=

Plotten Sie die Verteilung der Münzanzahl.

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]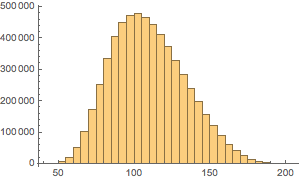

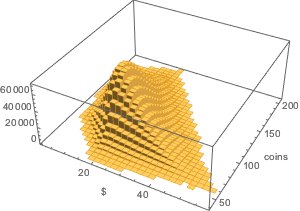
Out[20]=

Die bivariate Verteilung des Geldwerts versus die Münzanzahl im Sack.

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], 
 AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=

Wolfram Language™

Ermitteln Sie den Wert eines Sacks Münzen

Verwandte Beispiele