Wolfram Language™

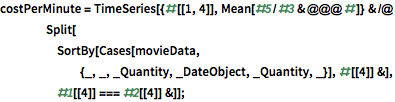
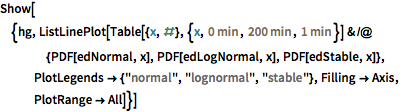
Berechnungsbasierte Filmologie

Untersuchen Sie mit der Wolfram Knowledgebase die Kosten pro Minute sowie das Einspielergebnis von Filmen, die seit dem Jahr 2000 herausgekommen sind. Untersuchen Sie außerdem die durchschnittliche Länge der Kinofilme, die einer stabilen Verteilung folgt, ungewöhnlich für vom Menschen geschaffene Objekte.

Verwenden Sie eine implizit definierte Entitätsklasse, um die Filme auszuwählen, die seit der Jahrtausendwende herausgekommen sind.

In[1]:=

Length[movies = EntityClass["Movie", EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}]] // EntityList]

Out[1]=

Ermitteln Sie Titel, Genre, Länge, Produktionsbudget und Einspielergebnis.

In[2]:=

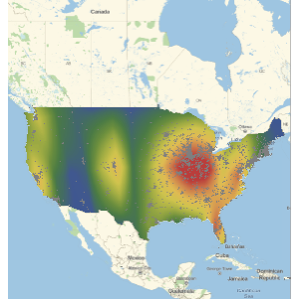
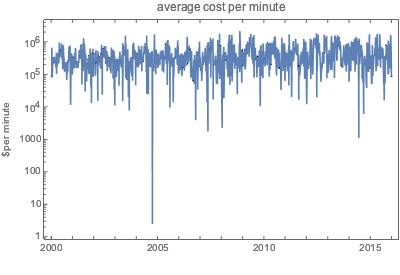
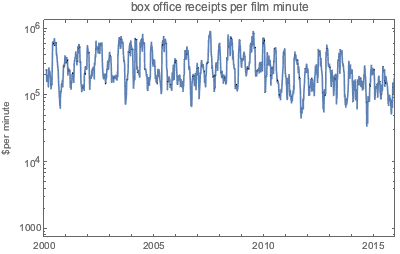
movieData = EntityValue[ movies, {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"], EntityProperty["Movie", "ProductionBudget"], EntityProperty["Movie", "DomesticBoxOfficeGross"]}];

Die Kosten pro Minute eines Kinofilms schwankt erheblich im Laufe der Zeit.

In[3]:=

costPerMinute = TimeSeries[{#[[1, 4]], Mean[#5/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _Quantity, _}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[4]:=

DateListLogPlot[costPerMinute, FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[4]=

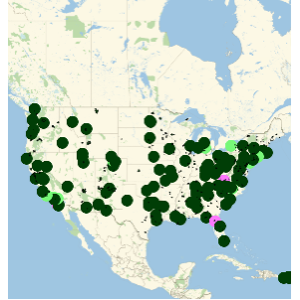
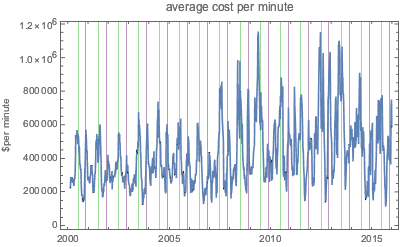
Im Monatsdurchschnitt kristallisieren sich jedoch einige periodische Regelmäßigkeiten heraus. Die grünen senkrechten Linien stehen für den amerikanischen Unabhängigkeitstag am 4. Juli, die violetten Linien markieren Thanksgiving.

In[5]:=

DateListPlot[MovingAverage[costPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "average cost per minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, GridLines -> {Join[{#, Darker[Green]} & /@ Table[DateObject[{y, 7, 4}], {y, 2000, 2015}], {#, Darker[Purple]} & /@ Table[DateObject@ WolframAlpha[ "Thanksgiving " <> IntegerString[y], {{"Result", 1}, "ComputableData"}], {y, 2000, 2015}]], None}]

Out[5]=

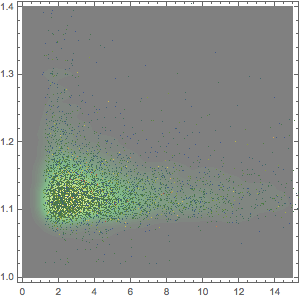
Die verkauften Tickets pro Minute ergeben eine noch stärker schwankende Funktion.

In[6]:=

profitPerMinute = TimeSeries[{#[[1, 4]], Mean[#6/#3 & @@@ #]} & /@ Split[SortBy[ Cases[movieData, {_, _, _Quantity, _DateObject, _, _Quantity}], \ #[[4]] &], #1[[4]] === #2[[4]] &]];

In[7]:=

DateListLogPlot[MovingAverage[profitPerMinute, Quantity[1, "Months"]], FrameLabel -> Automatic, PlotLabel -> "box office receipts per film minute", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}, PlotRange -> {{DateObject[{2000, 1, 1}], DateObject[{2015, 12, 31}]}, All}]

Out[7]=

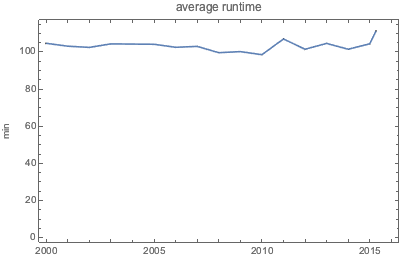
Die durchschnittliche Länge der Kinofilme hat sich über die letzten 15 Jahre ziemlich gleich gehalten.

In[8]:=

averageRuntimes = {#[[1, 1]], Mean[#[[All, -1]]]} & /@ Split[Sort[{DateObject[{#4["Year"]}], UnitConvert[#3, "Minutes"]} & @@@ Cases[movieData, {_, _, _Quantity, _DateObject, _, _}]], #1[[ 1]] === #2[[1]] &];

In[9]:=

DateListPlot[averageRuntimes, FrameLabel -> Automatic, PlotLabel -> "average runtime", AxesOrigin -> {DateObject[{2000, 1, 1}], 0}]

Out[9]=

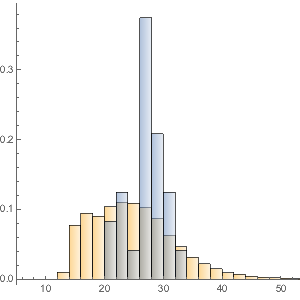
Im Gegensatz dazu ergibt die Verteilung der Filmlängen eine relativ ausgeglichene Verteilung.

In[10]:=

movieRuntimes = DeleteMissing[movieData[[All, 3]]];

In[11]:=

hg = Histogram[movieRuntimes, {1, 200, 5}, "PDF", AxesLabel -> Automatic]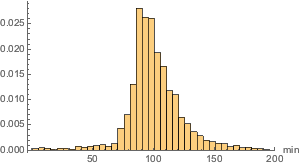

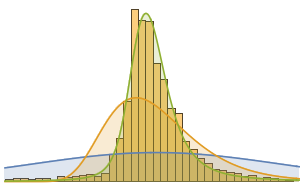
Out[11]=

Nach der Modellierung vieler eingebauter Verteilungen erscheint eine Lévy-stabile Verteilung am passendsten. In diesem Beispiel wurden eine Normalverteilung (Verteilung der Durchschnittswerte von Zufallsvariablen, die unabhängigen Verteilungen entnommen wurden), eine Lognormalverteilung (Verteilung des multiplikativen Produkts vieler unabhängiger positiver Zufallsvariablen) und eine alpha- stabile Verteilung modelliert.

In[12]:=

edNormal = EstimatedDistribution[movieRuntimes, NormalDistribution[\[Mu], \[Sigma]]]

Out[12]=

In[13]:=

edLogNormal = EstimatedDistribution[movieRuntimes, LogNormalDistribution[\[Mu], \[Sigma]]]

Out[13]=

In[14]:=

edStable = EstimatedDistribution[movieRuntimes, StableDistribution[1, \[Alpha], \[Beta], \[Mu], \[Sigma]]]

Out[14]=

Interessanterweise ist die alpha-stabile Verteilung visuell am passendsten.

In[15]:=

Show[{hg, ListLinePlot[ Table[{x, #}, {x, Quantity[0, "Minutes"], Quantity[200, "Minutes"], Quantity[1, "Minutes"]}] & /@ {PDF[edNormal, x], PDF[edLogNormal, x], PDF[edStable, x]}, PlotLegends -> {"normal", "lognormal", "stable"}, Filling -> Axis, PlotRange -> All]}]

Out[15]=

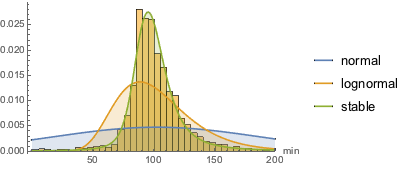
Nur wenige vom Menschen geschaffene Dinge folgen einer stabilen Verteilung. Ein Charakteristikum der stabilen Verteilung ist das Vorhandensein relativ großer Ausreißer, dei oft einige Male größer als der Mittelwert sind. Diese Eigenheit wird von Kinofilmen erfüllt. Nachstehend die längsten Filme, die nach dem 1. Januar 2000 herausgekommen sind.

In[16]:=

longest = EntityClass[ "Movie", {EntityProperty["Movie", "ReleaseDate"] -> Between[{DateObject[{2000}], DateObject[{2015}]}], EntityProperty["Movie", "Runtime"] -> TakeLargest[10]}] // EntityList

Out[16]=

Fassen Sie die Filme in einer Tabelle zusammen.

In[17]:=

With[{props = {EntityProperty["Movie", "Name"], EntityProperty["Movie", "Genres"], EntityProperty["Movie", "Runtime"], EntityProperty["Movie", "ReleaseDate"]}}, TextGrid[Prepend[EntityValue[longest, props], props], Dividers -> All, Alignment -> Left, Background -> {None, {LightBlue}}]] // TraditionalForm

Out[17]//TraditionalForm=