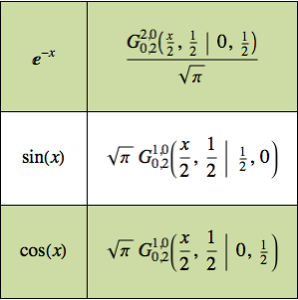그린 (Green) 함수를 사용한 초기값 문제 해결: Wolfram Language 11의 신기능

그린 (Green) 함수를 사용한 초기값 문제 해결

GreenFunction을 사용하여 비동차 미분 방정식의 초기값 문제를 해결합니다.

먼저, 그린의 함수를 계산합니다.

In[1]:=

gf[s_, t_] = 
 GreenFunction[{-u''[t] + u'[t] - 37/4 u[t], u[0] == 0, u'[0] == 0}, 
  u[t], {t, 0, \[Infinity]}, s]

Out[1]=

강제 함수를 정의합니다.

In[2]:=

f[t_] := Cos[a t]

강제 함수로 그린 함수를 합성곱하면 답을 얻을 수 있습니다.

In[3]:=

sol = Integrate[gf[s, t] f[s], {s, 0, \[Infinity]}, 
  Assumptions -> t > 0]

Out[3]=

DSolveValue에서 주어진 결과와 비교합니다.

In[4]:=

DSolveValue[{-u''[t] + u'[t] - 37/4 u[t] == f[t], u[0] == 0, 
   u'[0] == 0}, u[t], t] // FullSimplify

Out[4]=

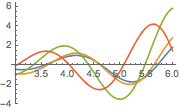
매개 변수 a의 다양한 값에 대한 솔루션을 플롯합니다.

In[5]:=

Plot[Table[sol, {a, 1, 4, 0.8}] // Evaluate, {t, 3, 6}]

Out[5]=