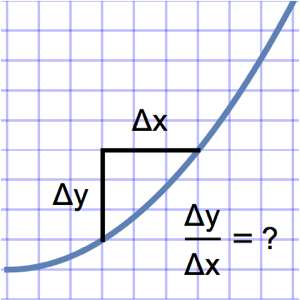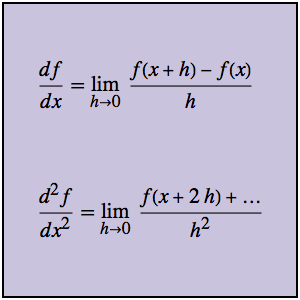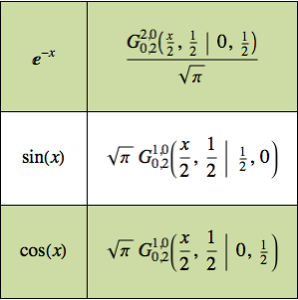처진 사슬 모델링: Wolfram Language 11의 신기능

‹›

처진 사슬 모델링

두 점 사이에 매달린 길이가 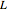인 체인 또는 케이블의 최소 포텐셜 에너지와 위치를 구합니다.

체인의 길이 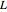, 왼쪽 끝의 높이 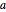, 오른쪽 끝의 높이 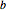에 대한 매개 변수값을 설정합니다.

In[1]:=

L = 4; a = 1; b = 3;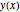

를 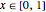인 수평 위치의 함수로 체인의 길이를 정합니다.

In[2]:=

xf = 1; nh = 201; h := xf/nh;

체인 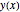의 높이에 대한 변수를 설정합니다.

In[3]:=

varsy = Array[y, nh + 1, {0, nh}];

위치 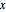에서의 기울기를 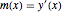로 나타나고 그에 대한 변수를 설정합니다.

In[4]:=

varsm = Array[m, nh + 1, {0, nh}];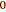

에서 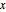까지의 부분적인 포텐셜 에너지를 로 표시합니다.

In[5]:=

varsv = Array[v, nh + 1, {0, nh}];

위치 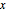에서의 체인의 길이를 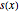로 나타나고 그에 대한 변수를 설정합니다.

In[6]:=

varss = Array[s, nh + 1, {0, nh}];

모든 변수를 연결합니다.

In[7]:=

vars = Join[varsm, varsy, varsv, varss];

여기서 목적은 전체 포텐셜 에너지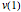을 최소화하는 것입니다.

In[8]:=

objfn = v[nh];

다음은 기하학으로부터의 경계값 제약 조건입니다.

In[9]:=

bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L};

상미분 방정식 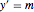, , 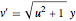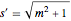을 이산화합니다.

In[10]:=

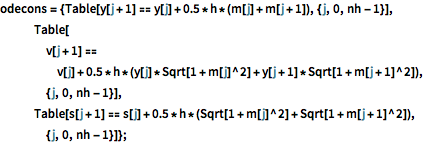
odecons = {Table[
    y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
   Table[v[j + 1] == 
     v[j] + 0.5*
       h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j, 
     0, nh - 1}], 
   Table[s[j + 1] == 
     s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0, 
     nh - 1}]};

변수에 대한 초기점을 선택합니다.

In[11]:=

tmin = If[b > a, 0.25 , 0.75]; init = 
 Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
  Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
  Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
    Abs[b - a]*((k/nh) - tmin), {k, 0, nh}], 
  Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];

제약 조건의 대상이 되는 전체 포텐셜 에너지를 최소화합니다.

In[12]:=

sol = FindMinimum[{objfn, Join[bndcons, odecons]}, 
   Thread[{vars, init}]];

솔루션의 점을 추출합니다.

In[13]:=

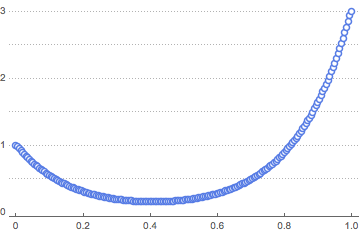
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];

최소 포텐셜 에너지를 가진 체인의 위치를 플롯합니다.

In[14]:=

ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]

Out[14]=

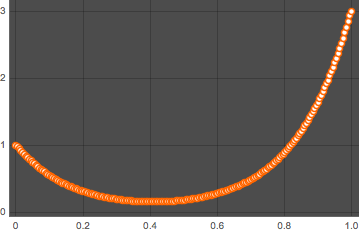
FindFit을 사용하여 현수 곡선에 결과를 맞춥니다.

In[15]:=

catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];

In[16]:=

fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]

Out[16]=

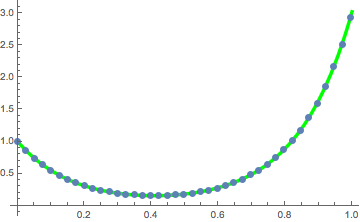
솔루션의 점과 현수 곡선을 함께 플롯합니다.

In[17]:=

Show[Plot[catenary[t] /. fitsol, {t, 0, 1}, 
  PlotStyle -> Directive[Green, Thickness[0.01]], 
  ImageSize -> Medium], 
 ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]

Out[17]=

Wolfram 언어™

처진 사슬 모델링

관련 예제