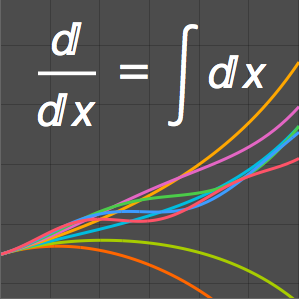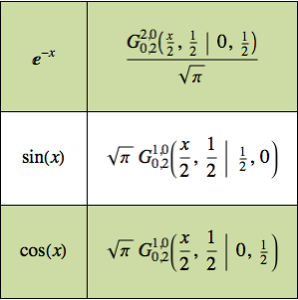Wolfram 언어™

램프 강제 함수를 사용한 상미분 방정식 해결

순수한 램프 응답을 계산합니다.

In[1]:=

sol = DSolveValue[{x''[t] + a^2 x[t] == Ramp[t - a], x[0] == 0, x'[0] == 0}, x[t], t, Assumptions -> a > 0] // FullSimplify

Out[1]=

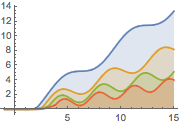
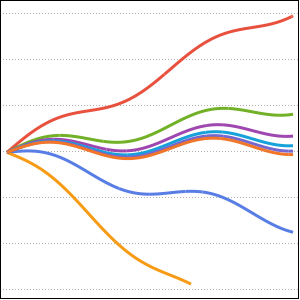
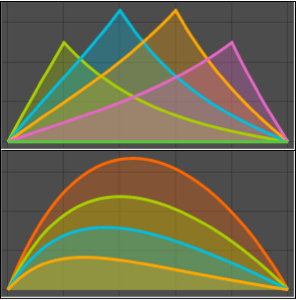
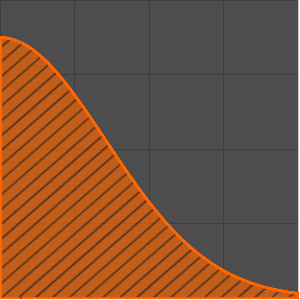
매개 변수 a의 다양한 값에 대한 솔루션을 플롯합니다.

In[2]:=

Plot[Table[sol, {a, 1, 2, 0.3}] // Evaluate, {t, -1, 15}, Filling -> Axis]

Out[2]=

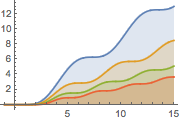
램프와 충격력을 결합합니다.

In[3]:=

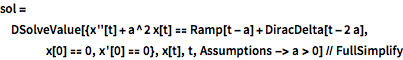
sol = DSolveValue[{x''[t] + a^2 x[t] == Ramp[t - a] + DiracDelta[t - 2 a], x[0] == 0, x'[0] == 0}, x[t], t, Assumptions -> a > 0] // FullSimplify

Out[3]=

In[4]:=

Plot[Table[sol, {a, 1, 2, 0.3}] // Evaluate, {t, -1, 15}, Filling -> Axis]

Out[4]=