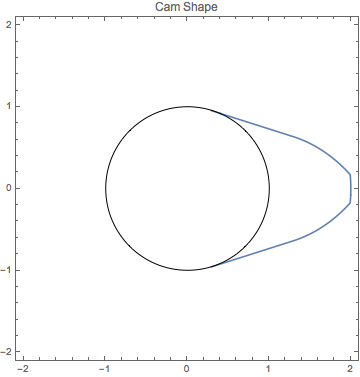
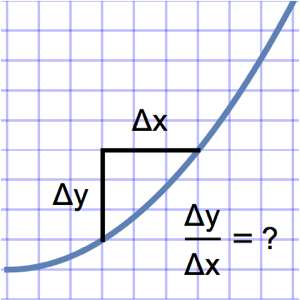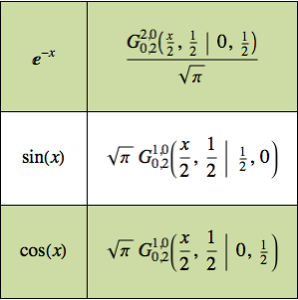캠의 형상 최적화: Wolfram Language 11의 신기능

‹›

캠의 형상 최적화

캠의 1 회전에 대한 밸브의 입구가 극대화되도록 캠의 반경에 제약 조건을 붙여 볼록 캠의 형상을 설계합니다.

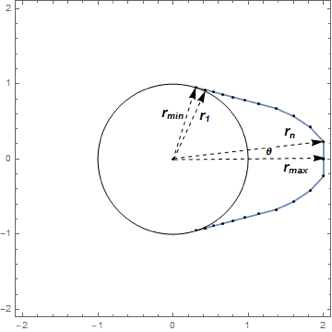
캠의 형상은 반경 r_min의 원주의 각도 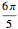의 원형이며, 나머지 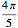에 대칭 형태로 간주합니다.

설계 변수 r_i, i=1, …, n은 각도 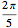, 즉 캠의 원형 부분이 아닌 상단의 반부에 분포한 등간격의 각도 θ에서의 캠의 반경을 나타냅니다.

In[1]:=

n = 100; vars = Array[r, n];

각각의 반경 r_i는 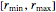구간에 존재해야 합니다.

In[2]:=

rmin = 1; rmax = 2;
varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];

위에서 정의된 각도 θ를 입력합니다.

In[3]:=

\[Theta] = 2 Pi/(5 (n + 1));

볼록 제약은 불평등계 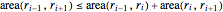에 의해 표현됩니다.

In[4]:=

convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <= 
   (1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[
      i + 1] Sin[\[Theta]];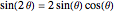

을 사용하면, 시스템을 아래와 같이 다시 표현할 수 있습니다. 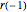은 캠의 원형 부분에 있는 점의 반경이므로 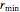과 동일함을 주목합니다.

In[5]:=

convexconstr = 
  Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <= 
     r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin, 
    r[0] -> rmin, r[n + 1] -> rmax};

반경의 변화율에 대한 제약은 매개 변수 α에서 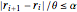로 표현 됩니다.

In[6]:=

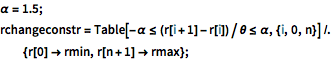
\[Alpha] = 1.5; rchangeconstr = 
 Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0, 
    n}] /. {r[0] -> rmin, r[n + 1] -> rmax};

목적 함수 (밸브 개방부)는 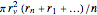, r_v는 밸브 값의 기하학에 관련된 상수로서 주어지며, 설계 변수 r_i 와 단순한 선형 관계를 갖는 것으로 가정됩니다.

In[7]:=

rv = 1;
objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];

변수의 초기점을 선택합니다.

In[8]:=

initpts = Table[.5 (rmin + rmax), {i, 1, n}];

극대화 문제를 해결합니다.

In[9]:=

sol = FindMaximum[
   Join[{objfun}, varbounds, convexconstr, rchangeconstr], 
   Thread[vars, initpts]];

최대 반경 중 일부는 최대의 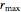입니다.

In[10]:=

Table[r[i], {i, 95, 100}] /. sol[[2]]

Out[10]=

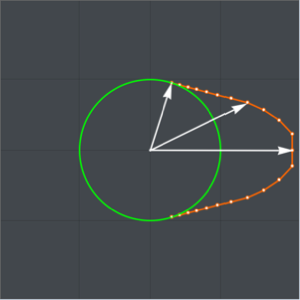
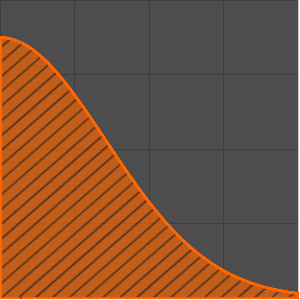
해를 플롯합니다.

전체 Wolfram 언어 입력 표시하기

In[11]:=

solpts1 = 
  Table[{r[i] Cos[-2. Pi/5 + \[Theta] i], 
      r[i] Sin[-2. Pi/5. + \[Theta] i]}, {i, -1, n + 2}] /. {r[-1] -> 
      rmin, r[0] -> rmin, r[n + 1] -> rmax, r[n + 2] -> r[n]} /. 
   sol[[2]];
solpts2 = Map[{#[[1]], -#[[2]]} &, Reverse@solpts1];
solpts = Join[solpts1, solpts2];
Show[ListLinePlot[solpts, PlotRange -> {{-2.1, 2.1}, {-2.1, 2.1}}, 
  PlotLabel -> "Cam Shape", AspectRatio -> 1, Axes -> False, 
  Frame -> True], Graphics[{Circle[{0., 0.}, 1.]}], 
 ImageSize -> Medium]

Out[11]=

Wolfram 언어™

캠의 형상 최적화

관련 예제