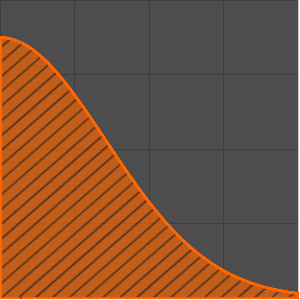
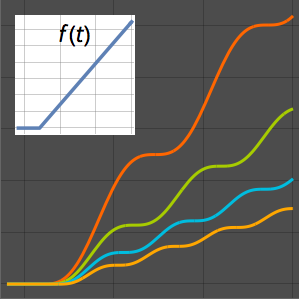
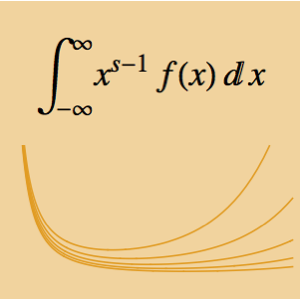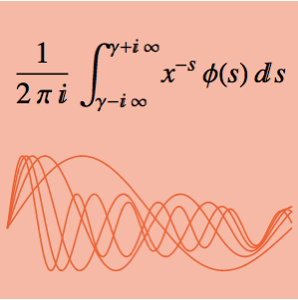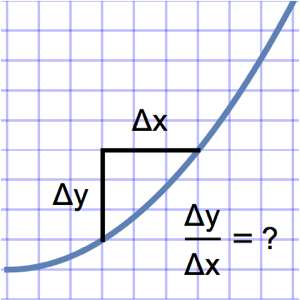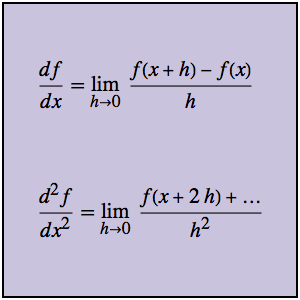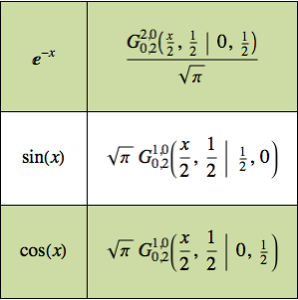등시강하곡선 문제 해결
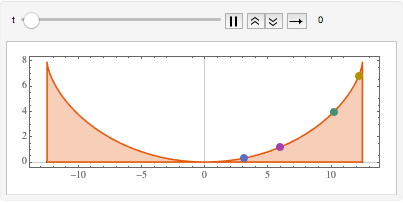
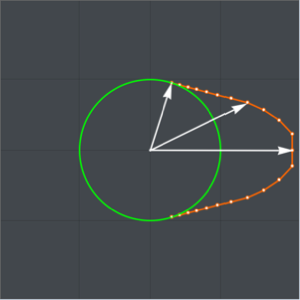
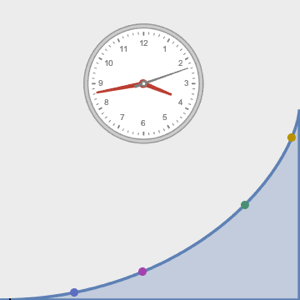
등시강하곡선 문제는 곡선위 임의의 장소에 위치해 있는 구슬이 모두 같은 시간에 바닥까지 떨어지는 곡선을 찾는 것입니다. 곡선의 호 길이와 속도 v에 대해 총 낙하 시간을 나타내면, 아벨 (Abel) 적분 방정식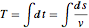 
이 됩니다. 관계 
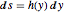에 의해 미지의 함수 
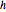를 정의하고, 에너지 보존 방정식 
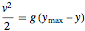를 사용하면 다음의 명시적인 방정식이됩니다.
In[1]:=
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);DSolveValue를 사용하여 적분 방정식을 풉니다.
In[2]:=
dsdy = DSolveValue[abeleqn, h[y], y]Out[2]=
관계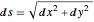 
를 사용하여 
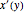에 대해 해결합니다.
In[3]:=
dxdy = Sqrt[dsdy^2 - 1]Out[3]=
곡선을 원점에서 시작하여 적분하면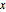 
를 
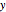의 함수로 얻을 수 있습니다. 가정은 피적분 함수가 실수값임을 보장하는 것에 주목할 필요가 있습니다.
In[4]:=
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]Out[4]=
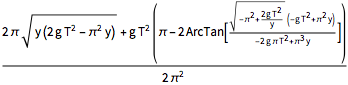
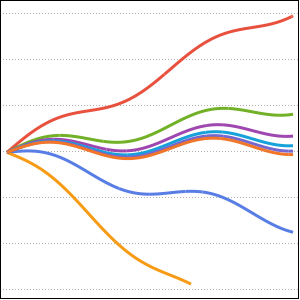
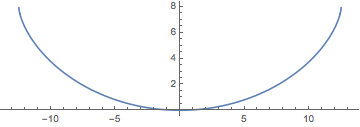
2초의 하강 시간을 이용하여 중력 가속도의 값에 대입하여 등시강하곡선의 최대 곡선을 플롯합니다. (브랜치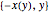 
는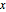 
의 도함수에 대한 답 
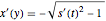에서 유래)
In[5]:=
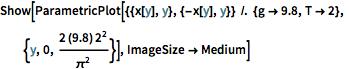
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]Out[5]=
변수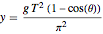 
을 변화 시키면 
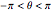에 있어서의 단순하고 비특이적 곡선의 매개 변수를 제공합니다.
In[6]:=
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;에너지 보존 방정식과 연쇄 율법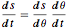 
를 결합하면 
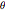를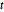 
의 함수로 하는 다음의 미분 방정식이 생성되며, 수치적 풀이가 가능합니다.
In[7]:=
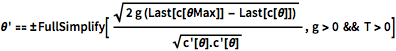
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]Out[7]=
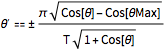
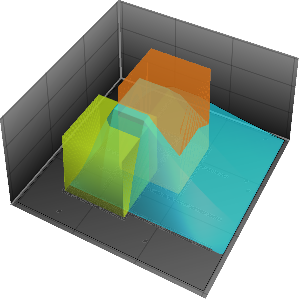
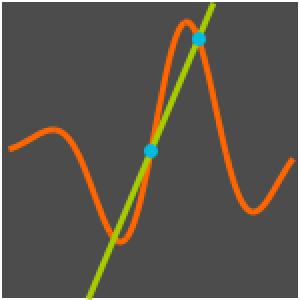
등시강하곡선을 따라 운동을 시각화합니다.
