在非笛卡尔坐标系下计算面积和体积
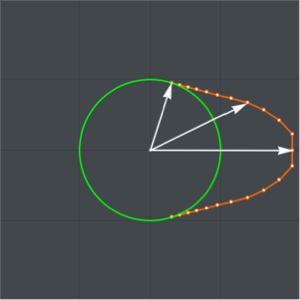
通过围绕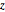 
轴旋转曲线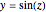 
定义出的这个“坚果”很容易在柱坐标中参数化.
In[1]:=
ParametricPlot3D[
CoordinateTransform[ "Cylindrical" -> "Cartesian", {Sin[z], t, z}] //
Evaluate, {z, 0, Pi}, {t, 0, 2 Pi}, PlotTheme -> "Business"]Out[1]=
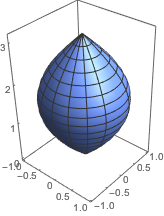
用 Area 直接在柱坐标里求表面积.
In[2]:=
Area[{Sin[z], t, z}, {z, 0, Pi}, {t, 0, 2 Pi}, "Cylindrical"]Out[2]=
Volume（体积）也可以在非笛卡尔坐标系里计算.
In[3]:=
Volume[{r Sin[z], t, z}, {z, 0, Pi}, {t, 0, 2 Pi}, {r, 0,
1}, "Cylindrical"]Out[3]=
通过使用 RegionMeasure，可以在任何维数下进行这些计算.
In[4]:=
RegionMeasure[{Sin[z], t,
z}, {{z, 0, Pi}, {t, 0, 2 Pi}}, "Cylindrical"]Out[4]=
In[5]:=
RegionMeasure[{r Sin[z], t,
z}, {{z, 0, Pi}, {t, 0, 2 Pi}, {r, 0, 1}}, "Cylindrical"]Out[5]=
