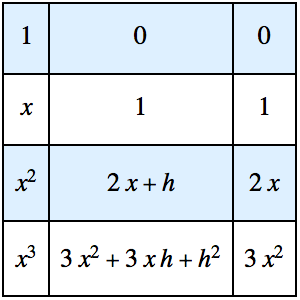
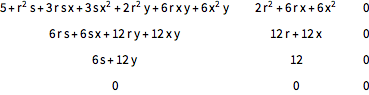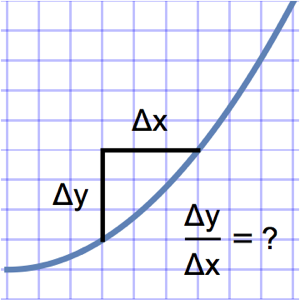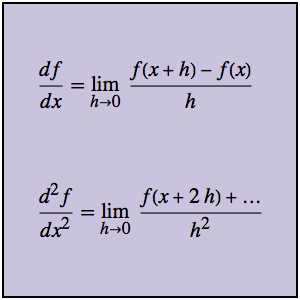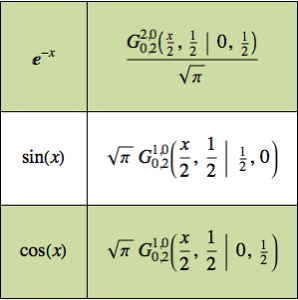差分商を計算する
Wolfram言語はよく知られている1変量差分商だけでなく,多変量や高次の差分商も計算できる.
In[1]:=
DifferenceQuotient[f[x], {x, h}]Out[1]=
2次の差分商は1次の商の差分商である.
In[2]:=
DifferenceQuotient[f[x], {x, 2, h}]Out[2]=
In[3]:=
DifferenceQuotient[f[x], {x, h}];
DifferenceQuotient[f[x], {x, 2, h}];
% == DifferenceQuotient[%%, {x, h}]Out[3]=
多変量の差分商を計算する.
In[4]:=
DifferenceQuotient[(x + y + 1)/(((x^2 + 3) (y + 5))), {x, h}, {y, k}]Out[4]=
降順の多項式を生成する,多項式の昇順の差分商の表を生成する.
In[5]:=
Grid[Table[
DifferenceQuotient[x^3 y^2 + 5 x y + 11, {x, i, r}, {y, j, s}], {i,
4}, {j, 3}], Spacings -> {2, 1}]Out[5]=