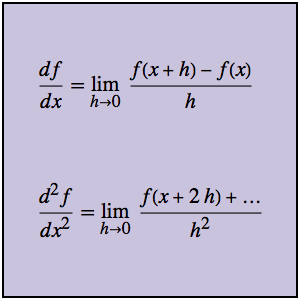Calcule uma derivada usando primeiros princípios
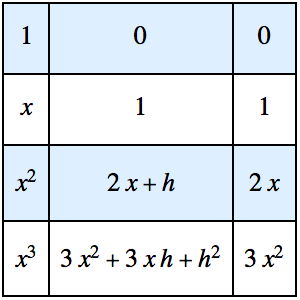
Os quocientes de diferença podem ser utilizados diretamente para calcular não apenas a primeira derivada, mas tambén derivadas de ordem superior. Considere primeiro l função g e seu quociente de diferença associado.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
Considerando o limite do quociente de diferença da primeira derivada.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
A segunda derivada pode ser calculada diretamente a partir do segundo quociente de diferença, sin nunca fazer referência a primeira derivada.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
O limite como 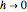 é a segunda derivada.
é a segunda derivada.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
O quociente de diferença da primeira derivada é uma função diferente do quociente de diferença de segunda ordem de g, mas seu limite também é a segunda derivada.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=