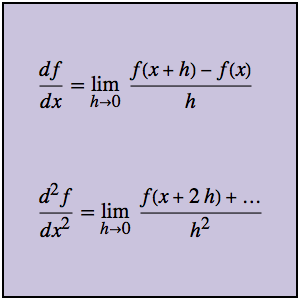用第一性原理计算导数
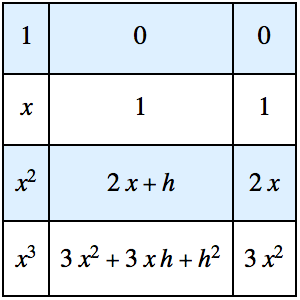
差商不仅可以直接用于计算一阶导数，它也可以直接用于高价导数的计算. 先考虑函数 g 及其相关的差商.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
对差商取极限即给出一阶导数.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
可以直接根据二阶差商来计算二阶导数，而不必去参引一阶导数.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
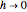时的极限便是二阶导数.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
g 的一阶导数的差商与二阶差商是不同的函数，但它的极限也是二阶导数.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=
