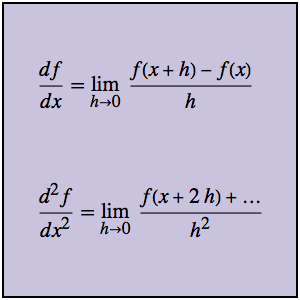제1 원칙을 사용한 도함수 평가
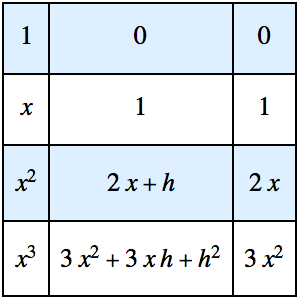
차분몫은 일차 도함수 뿐만 아니라 고차 도함수를 직접 계산하는데도 사용할 수 있습니다. 우선 함수 g와 관련하여 차분몫을 고려해 봅니다.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
차분몫의 극한을 취하면 1차 도함수가 주어집니다.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
이차 도함수는 일차 도함수를 참조하지 않고도 이차 차분몫에서 직접 계산할 수 있습니다.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
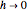일때의 극한이 이차 도함수입니다.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
1차 도함수의 차분몫은 g의 2차 차분몫과 다른 함수이지만, 그 극한은 역시 2차 도함수입니다.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=
